题目内容
设函数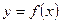 定义在
定义在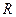 上,对于任意实数
上,对于任意实数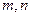 ,恒有
,恒有
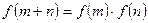 ,且当
,且当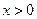 时,
时,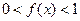
(1)求证: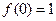 且当
且当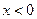 时,
时,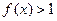
(2)求证: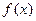 在
在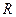 上是减函数;
上是减函数;
(3)设集合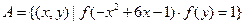 ,
,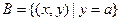 ,
,
且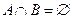 , 求实数
, 求实数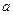 的取值范围。
的取值范围。
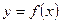 定义在
定义在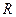 上,对于任意实数
上,对于任意实数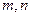 ,恒有
,恒有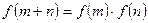 ,且当
,且当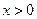 时,
时,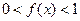
(1)求证:
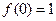 且当
且当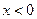 时,
时,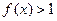
(2)求证:
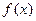 在
在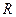 上是减函数;
上是减函数;(3)设集合
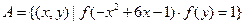 ,
,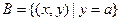 ,
,且
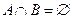 , 求实数
, 求实数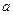 的取值范围。
的取值范围。(3)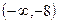
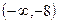
(1)证明: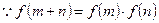 ,
,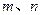 为任意实数,
为任意实数,
取 ,则有
,则有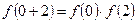
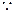 当
当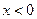 时,
时,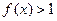 ,
,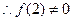 ,
,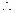
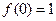 ……2分
……2分
当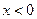 时,
时,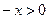
 ,则
,则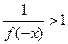
取 则
则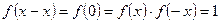
则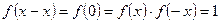
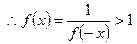 ……6分
……6分
(2)证明:由(1)及题设可知,在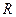 上
上
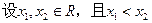 ,
,

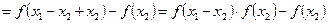
 …………8分
…………8分


所以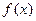 在
在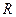 上是减函数…………9分
上是减函数…………9分
(3)解:在集合 中
中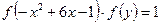
由已知条件,有
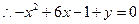 ,即
,即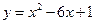 …………12分
…………12分
在集合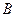 中,有
中,有
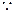
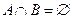 ,则抛物线
,则抛物线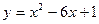 与直线
与直线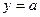 无交点
无交点
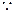
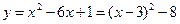 ,
, ,
,
即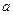 的取值范围是
的取值范围是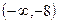 …………15分
…………15分
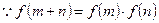 ,
,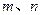 为任意实数,
为任意实数,取
 ,则有
,则有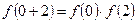
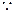 当
当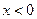 时,
时,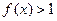 ,
,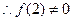 ,
,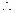
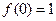 ……2分
……2分当
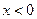 时,
时,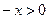
 ,则
,则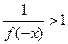
取
 则
则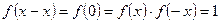
则
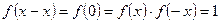
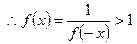 ……6分
……6分(2)证明:由(1)及题设可知,在
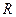 上
上
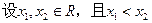 ,
,

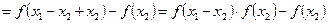
 …………8分
…………8分

所以
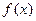 在
在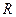 上是减函数…………9分
上是减函数…………9分(3)解:在集合
 中
中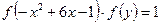
由已知条件,有

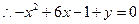 ,即
,即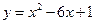 …………12分
…………12分在集合
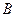 中,有
中,有
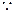
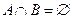 ,则抛物线
,则抛物线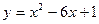 与直线
与直线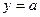 无交点
无交点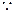
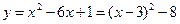 ,
, ,
,
即
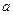 的取值范围是
的取值范围是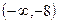 …………15分
…………15分
练习册系列答案
相关题目
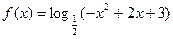
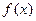 的定义域; (2)求
的定义域; (2)求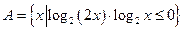
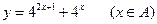 的值域
的值域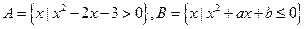 ,
,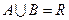 ,
,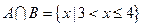 ,则
,则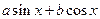 的最小值是多少?
的最小值是多少?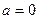 时,求
时,求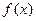 的极值;
的极值;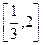 上是增函数,求实数
上是增函数,求实数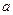 的取值范围
的取值范围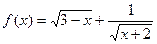 的定义域为集合A,
的定义域为集合A,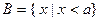
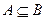 ,求a
,求a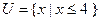 ,a=
,a=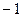 ,求
,求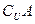 及
及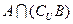
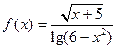 的定义域:
的定义域: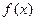 为一次函数,
为一次函数,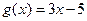 ,且满足
,且满足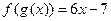
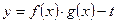 有零点,求
有零点,求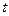 的取值范围.
的取值范围.  的定义域
的定义域