题目内容
对于给定数列
，如果存在实常数
,使得
对于任意
都成立，我们称数列是 “M类数列”．
（I）若
，
，，数列
、
是否为“M类数列”？
若是，指出它对应的实常数
，若不是，请说明理由；
（II）若数列满足
，
，
为常数．
求数列前
项的和；
是否存在实数，使得数列是“M类数列”，如果存在，求出；如果不存在，说明理由.
同下
解析:
（I）因为
则有
故数列
是“M类数列”， 对应的实常数分别为
． ……………………………2分
因为
，则有
故数列
是“M类数列”， 对应的实常数分别为
． ……………………………4分
（II）（1）因为 
则有
，
，
， 
……………………………….6分
故数列前
项的和
+
+
+
+
………………9分
若数列是“M类数列”， 则存在实常数
使得
对于任意都成立，………………………………………….10分
且有
对于任意都成立，
因此
对于任意都成立，
而
，且
则有
对于任意都成立，可以得到
，………………………………………12分
①当
时，
，
，
，经检验满足条件.
②当
时，
，
，
经检验满足条件.
因此当且仅当或
，时，数列
也是“M类数列”.对应的实常数分别为
, 或
． ………………………………………………………………14分
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
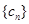，如果存在实常数
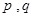使得
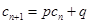对于任意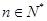
都成立，我们称数列
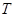数列”．
，
，
、
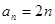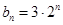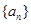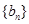是否为“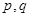
，若不是，请说明理由；
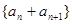也是“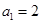
，
，
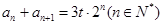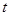为常数．求数列
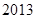项的和．
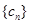，如果存在实常数
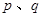，使得
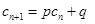对于任意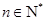
都成立，我们称数列
，
，
、
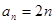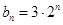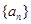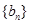是否为“M类数列”？若是，指出它对应的实常数
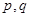，若不是，请说明理由；
，
．
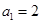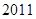项的和．
.
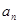，如果存在实常数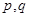
，使得
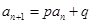对于任意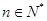
都成立，我们称数列
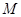类数列”．
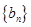是 “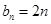
，求它对应的实常数
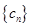满足
，
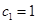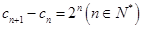，求数列
，如果存在实常数
，使得
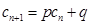对于任意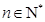
都成立，我们称数列
，
，
、
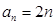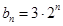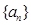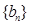是否为“M类数列”？若是，指出它对应的实常数
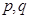，若不是，请说明理由；
，
．
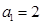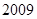项的和．(2)已知数列
.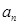