Question

已知AB⊥平面BCD，如图所示，AB=2，CD=5，△BCD的面积为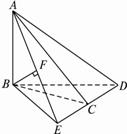，求点B到平面ACD的距离.

Answer 1

解法一：过B点作BE⊥CD于E，连结AE.则AE⊥CD，所以CD⊥平面ABE.所以平面ABE⊥平面ACD.?

过B作AE的垂线BF，垂足为F，则BF⊥平面ACD.?

所以BF的长为B点到平面ACD的距离.?

因为S_△BCD=,CD=5,所以BE=.?

又因为AB=2，所以AE=4.?

在Rt△ABE中，由面积相等有BF、5AE=AB、5BE,?

得BF=,所以B点到平面ACD的距离为.?

解法二：(等积法)过B点作BE⊥CD于E点，连结AE，则AE⊥CD，所以∠AEB为二面角A-CD-B的平面角.?

因为BE=，AE=4，S_△BCD =S_△ACD 、5cosθ,?

所以.?

由于V_A—BCD?=V_B—ACD ,,?

所以h=,h为点B到平面ACD的距离.?

所以B到平面ACD的距离为.