题目内容
设等差数列:2,a+2,3a,…的前n项和为Sn,则
+
+…+
的值是
.
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S100 |
| 100 |
| 101 |
| 100 |
| 101 |
分析:利用等差数列的中项公式列出关于a的等式,求出首项a,利用等差数列的前n项和公式求出Sn=n(n+1)得到
,将其裂成两项的差,利用裂项求和的方法求出和.
| 1 |
| Sn |
解答:解:∵等差数列前三项为2,a+2,3a,
∴2×(a+2)=2+3a,
∴a=2,
公差d=4-2=2
所以等差数列2,4,6,…的前n项和Sn=
,即Sn=n(n+1)
于是
=
=
-
,
则
+
+…+
=(1-
)+(
-
)+(
-
)+…+(
-
)=1-
=
故答案为:
.
∴2×(a+2)=2+3a,
∴a=2,
公差d=4-2=2
所以等差数列2,4,6,…的前n项和Sn=
| n(2+2n) |
| 2 |
于是
| 1 |
| Sn |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S100 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 100 |
| 1 |
| 101 |
| 1 |
| 101 |
| 100 |
| 101 |
故答案为:
| 100 |
| 101 |
点评:求数列的前n项和,应该先求出数列的通项,根据通项的特点选择合适的求和方法.常用的求和方法有:公式法、错位相减法、裂项相消法、倒序相加法、分组法.

练习册系列答案
相关题目
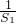 +
+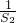 +…+
+…+ 的值是________.
的值是________. +
+ +…+
+…+ 的值是 .
的值是 .