题目内容
已知正方形ABCD—A1B1C1D1中，E、F分别为AB1、BC1上两点，且B1E=C1F，求证：EF∥平面AC.证明:如图，
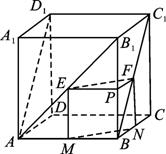
过E、F分别作AB、BC的垂线EM、FN交AB、BC于M、N，连结MN.
∵BB1⊥平面AC，
∴BB1⊥AB，BB1⊥BC.
∴EM∥BB1，FN∥BB1.
∴EM∥FN.
∵AB1=BC1，B1E=C1F，∴AE=BF.
又∠B1AB=45°=∠C1BC，
∴Rt△AME≌Rt△BNF.∴EM=FN.
∴四边形MNFE是平行四边形.∴EF∥MN.
而MN
平面AC，∴EF∥平面AC.
练习册系列答案
相关题目
已知正方形ABCD边长为1，则|
+
+
|=（ ）
| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|
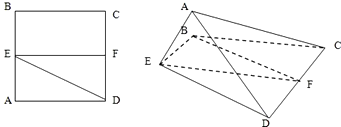已知正方形ABCD．E、F分别是AB、CD的中点，将△ADE沿DE折起，如图所示，记二面角A-DE-C的大小为θ（0＜θ＜π）．
（2008•虹口区二模）（理）已知正方形ABCD的边长为1，PD⊥平面ABCD，PD=3，