题目内容
已知几何体M的正视图是一个面积为2 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
A.6 和 和  | B.6 +4 +4 和 和  |
C.6 +4 +4 和 和  | D.4( + + )和 )和  |
C
解析试题分析:根据题意,由于几何体M的正视图是一个面积为2 的半圆,俯视图是正三角形,那么这个几何体是由一个三棱锥和一个半球体的组合体,球的半径为2,三棱锥的高为2,底面是正三角形,边长为4,则可知其表面积和体积为6
的半圆,俯视图是正三角形,那么这个几何体是由一个三棱锥和一个半球体的组合体,球的半径为2,三棱锥的高为2,底面是正三角形,边长为4,则可知其表面积和体积为6 +4
+4 和
和
 ,故选C.
,故选C.
考点:三视图的运用
点评:解决的关键是利用已知的三视图来分析得到简单几何体,结合几何体的体积和表面积公式求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个棱锥的三视图如图(尺寸的长度单位为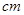 ),则该棱锥的体积是
),则该棱锥的体积是 
A. | B.8 |
| C.4 | D. |
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6则该球的表面积为
A.16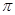 | B.24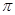 | C.32 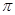 | D.48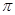 |
已知某几何体的三视图如图所示,若该几何体的体积为24,则正视图中a的值为
| A.8 | B.6 |
| C.4 | D.2 |
已知一个棱长为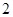 的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是
的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是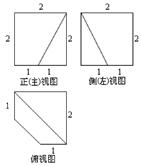
| A.8 | B.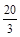 |
C.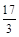 | D.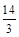 |
一个几何体的三视图如右图所示,则它的体积为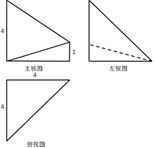
A.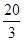 | B.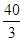 |
C.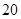 | D.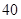 |
一个几何体的三视图如图所示,则该几何体的体积为 ( ) 
A. | B. | C. | D. |
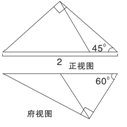
 的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去
的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去 个三棱锥后 ,剩下的几何体的体积是( )
个三棱锥后 ,剩下的几何体的体积是( )


