Question

如下图，在正方体ABCD-A₁B₁C₁D₁中,P为对角线BD₁的三等分点，则P到各顶点距离的不同取值有(     )

A．6个    B．5个             C．4个 D．3个

 

Answer 1

【答案】

C

【解析】

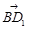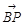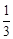
试题分析：建立如图所示的空间直角坐标系，不妨设正方体的棱长|AB|=3，即可得到各顶点的坐标，利用两点间的距离公式即可得出, 则A（3，0，0），B（3，3，0），C（0，3，0），D（0，0，0），A1（3，0，3），B1（3，3，3），C1（0，3，3），D1（0，0，3），∴=（-3，-3，3），设P（x，y，z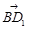），∵==（-1，-1，1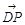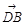），∴=+(−1，−1，1)=（2，2，1）．∴|PA|=|PC|=|PB₁|=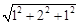=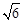,|PD|=|PA₁|

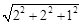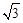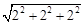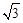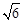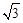=|PC₁|==3，|PB|=，|PD₁|==2,故P到各顶点的距离的不同取值有,3, ，2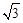,共4个,故选C．

考点：点、线、面间的距离计算．