题目内容
(
吉林实验中学模拟)如下图,在正方体ABCD- 中,M是棱AB的中点.
中,M是棱AB的中点.
(1)
求证:BC∥平面 ;
;
(2)
求二面角 -
- -C的大小.
-C的大小.

答案:略
解析:
解析:
|
解析:解法一: (1)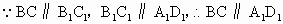 . .
又 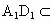 平面 平面 , ,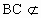 平面 平面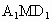 , ,
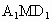 ; (5分) ; (5分)
(2) 设平面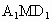 与棱DC相交于点N,连结 与棱DC相交于点N,连结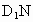 ,则点N是DC的中点. ,则点N是DC的中点.
 , ,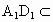 平面 平面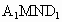 ,∴平面 ,∴平面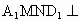 平面 平面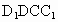 ,且 ,且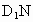 是交线. 是交线.
过点 C作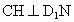 于H点,则CH⊥平面 于H点,则CH⊥平面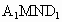 ,再过H作HO⊥ ,再过H作HO⊥ 于点O, 于点O,
连结 CO,根据三垂线定理得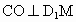 ,从而 ,从而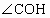 是二面角C- 是二面角C- -N,也就是所求二面角 -N,也就是所求二面角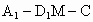 的补二面角的平面角. (8分) 的补二面角的平面角. (8分)
设正方体的棱长为 2,则在 中,由于 中,由于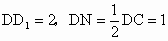 ,所以有 ,所以有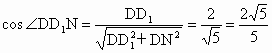 . .
在 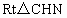 中,由于 中,由于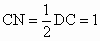 , ,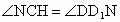 ,所以有 ,所以有
又由于可求得
所以在 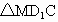 中,有 中,有
进而有 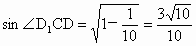 . .
根据三角形面积公式得
从而在 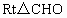 中, 中,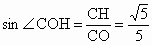 , ,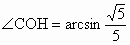 . .
因此所求的二面角 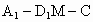 的大小为 的大小为 . (12分) . (12分)
解法二:分别以直线 DA、DC、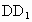 为x、y、z轴建立空间直角坐标系D-xyz,并设正方体的棱长为2,则相关点的坐标分别为 为x、y、z轴建立空间直角坐标系D-xyz,并设正方体的棱长为2,则相关点的坐标分别为 (2,0,2), (2,0,2),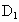 (0,0,2),C(0,2,0),M(2,1,0), (6分) (0,0,2),C(0,2,0),M(2,1,0), (6分)
设 n=(x,y,z)是平面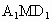 的法向量, 的法向量,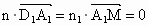 . .
而且 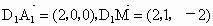 , ,
所以有  即 即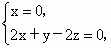
令 z=1,则y=2x,x=0,从而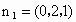 . (8分) . (8分)
再设 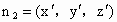 是平面 是平面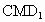 的法向量, 的法向量,
则 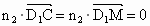 , ,
而且 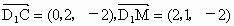 , ,
所以有 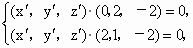 即 即
令 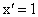 ,则 ,则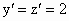 ,从而 ,从而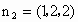 . .
设 θ是所求二面角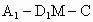 的平面角,则θ是钝角,并且有 的平面角,则θ是钝角,并且有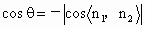 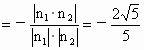 , ,
即 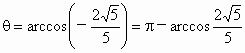 为所求. (12分) 为所求. (12分) |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(
吉林实验中学模拟)若 展开式中
展开式中 的系数等于
的系数等于 的系数的4倍,则n等于
的系数的4倍,则n等于
[
]|
A .7 |
B .8 |
C .9 |
D .10 |
(
吉林实验中学模拟)如下图,正四棱柱 中,
中, ,则异面直线
,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为

[
]|
A . |
B . |
C . |
D . |









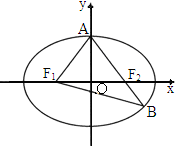
 (a>b>0),
(a>b>0), 、
、 分别为椭圆的左、右焦点,A为椭圆的上顶点,直线
分别为椭圆的左、右焦点,A为椭圆的上顶点,直线 交椭圆于另一点B.
交椭圆于另一点B.
 ,求椭圆的离心率;
,求椭圆的离心率;
 ,求椭圆的方程.
,求椭圆的方程.