题目内容
两圆C1：x2+y2=1，C2：（x-3）2+（y-4）2=16的公切线共有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
考点：两圆的公切线条数及方程的确定
专题：计算题,直线与圆
分析：分别求出圆心和半径，考查两圆的圆心距正好等于两圆的半径之和，故两圆相外切，即可得出结论．
解答：解：由题意，圆心C1（0，0），半径为1，圆心C2（3，4），半径为4，
两圆的圆心距为5，正好等于两圆的半径之和，
故两圆相外切，故两圆的公切线有3条，
故选：C．
两圆的圆心距为5，正好等于两圆的半径之和，
故两圆相外切，故两圆的公切线有3条，
故选：C．
点评：本题考查两圆的位置关系，两圆相外切的充要条件是：两圆的圆心距等于两圆的半径之和．
练习册系列答案
相关题目
已知直角梯形ABCD，AB⊥AD，CD⊥AD，AB=2AD=2CD=2，沿AC折叠成三棱锥，当三棱锥体积最大时，此时三棱锥外接球的体积是 （ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、2π |
已知点A（2，0），B（-2，4），C（5，8），若线段AB和CD有相同的垂直平分线，则点D的坐标是（ ）
| A、（6，7） | B、（7，6） | C、（-5，-4） | D、（-4，-5） |
过点（1，1）的直线与圆x2+y2-4x-6y+4=0相交于A，B两点，则|AB|的最小值为（ ）
A、2
| ||
| B、4 | ||
C、2
| ||
| D、5 |
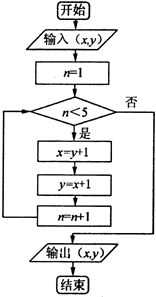已知某算法的流程图如图所示，输入的数x和y为自然数，若已知输出的有序数对为（13，14），则开始输入的有序数对（x，y）可能为（ ）| A、（6，7） | B、（7，6） | C、（4，5） | D、（5，4） |
执行如图所示的程序框图，若输入a，b的值分别为log34和log43，则输出S=（ ）
| A、0 | B、1 | C、2 | D、-1 |