题目内容

已知向量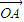=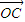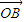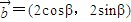，==，其中O为坐标原点，且0＜α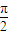＜＜β＜π
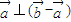（1）若，求β-α的值；
（2）若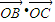=2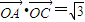，，求△OAB的面积S．
【答案】分析：（1）两个向量垂直的充要条件是这两个向量的数量积为0，将和用坐标表示，求其数量积，再倒用两交差的余弦公式即可
（2）由=2，，可得OA⊥OB，∴△OAB的面积为，求模代入即可
解答：解：（1）∵∴
∴2cosαcosβ+2sinαsinβ-1=0
即
∵∴0＜β-α＜π∴
（2）∵，
∴
∴
∴
∴
∴
点评：本题综合考查了向量数量积的运算性质和三角变换公式的应用，解题时要耐心细致，认真观察
练习册系列答案
相关题目
（1）已知向量
a
、
b
的模都是2，其夹角为60°，当
OP
=
10
a
+2
b
，
OQ
=-2
a
+
10
b
时，求P，Q两点间的距离；
（2）设向量
a
和
b
的长度分别为4和3，夹角为60°，求|
a
+
b
|的模．
已知向量
m
=（sinωx，1），
n
=（
3
Acosωx，
A
2
cos2ωx）（A＞0，ω＞0），函数f（x）=
m
•
n
的最大值为3，且其图象相邻两条对称轴之间的距离为π．
（I）求函数f（x）的解析式；
（II）将函数y=f（x）的图象向左平移
π
6
个单位，再将所得图象上各点的横坐标缩短为原来的
1
2
倍，纵坐标不变，得到函数y=g（x）的图象．
（1）求函数g（x）的单调递减区间；
（2）求函数g（x）在[
π
4
，
π
2
]上的值域．
已知向量
a
=（cosωx，cosωx），
b
=（
3
sinωx，cosωx），其中0＜ω＜2，f（x）=
a
•
b
+
1
2
，其图象的一条对称轴为x=
π
6
．
（1）求f（x）的表达式；
（2）在△ABC中，a，b，c分别为角A，B，C的对边，S为其面积，若f(
A
2
)=2 ， b=2 ， S=2
3
，求a的值．
已知向量
a
=(sin
x
3
，
3
cos
x
3
)，
b
=(1，1)，函数f(x)=
a
•
b
cos
x
3
．
（1）将f（x）写成Asin（ωx+φ）+B的形式，并求其图象的对称中心；
（2）如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为x，试求x的取值范围及此时函数f（x）的值域．
已知向量
a
、
b
的模都是2，其夹角为60°，又知
OP
=3
a
+2
b
，
OQ
=
a
+3
b
，则P、Q两点间的距离为（　　）
A、2
3
B、
3
C、2
2
D、
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网