题目内容
由曲线y=
与直线x=4,y=0围成的曲边梯形的面积为( )
| x |
分析:曲线y=
与直线x=4,y=0围成的曲边梯形的面积可用定积分计算,先求出图形横坐标范围,再求
dx即可.
| x |
| ∫ | 0 4 |
| x |
解答:解:由曲线y=
与直线x=4,y=0围成的曲边梯形的面积为:
dx=
x
|04=
×4
=
故选B.
| x |
| ∫ | 4 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 16 |
| 3 |
故选B.
点评:本题考查定积分在求面积中的应用,解答本题关键是根据题设中的条件建立起面积的积分表达式,再根据相关的公式求出积分的值,用定积分求面积是其重要运用,掌握住一些常用函数的导数的求法是解题的知识保证.

练习册系列答案
相关题目
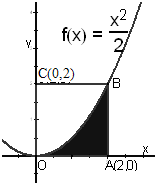 如图所示,计算图中由曲线y=
如图所示,计算图中由曲线y=