题目内容
【题目】已知左、右焦点分别为F1（﹣c，0），F2（c，0）的椭圆 
过点 
，且椭圆C关于直线x=c对称的图形过坐标原点．
（I）求椭圆C的离心率和标准方程．
（II）圆 
与椭圆C交于A，B两点，R为线段AB上任一点，直线F1R交椭圆C于P，Q两点，若AB为圆P1的直径，且直线F1R的斜率大于1，求|PF1||QF1|的取值范围．
【答案】解：（Ⅰ）∵椭圆C过点 
，∴ 
，① ∵椭圆C关于直线x=c对称的图形过坐标原点，∴a=2c，
∵a2=b2+c2 ， ∴ 
，②
由①②得a2=4，b2=3，a=2，c=1，
∴椭圆C的离心率 
，标准方程为 
．
（Ⅱ）因为AB为圆P1的直径，所以点P1
为线段AB的中点，
设A（x1 ， y1），B（x2 ， y2），则，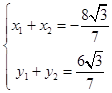 
，又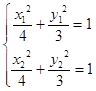 
，
所以 
，则（x1﹣x2）﹣（y1﹣y2）=0，故 
，则直线AB的方程为 
，即 
．
代入椭圆C的方程并整理得 
，
则 
，故直线F1R的斜率 
．
设F1R：y=k（x+1），由 
，得（3+4k2）x2+8k2x+4k2﹣12=0，
设P（x3 ， y3），Q（x4 ， y4），则有 
， 
．
又 
， 
，
所以|PF1||QF1|=（1+k2）|x3x4+（x3+x4）+1|= 
，
因为 
，所以 
，
即|PF1||QF1|的取值范围是 
【解析】（Ⅰ）利用椭圆C过点 
，∵椭圆C关于直线x=c对称的图形过坐标原点，推出a=2c，然后求解椭圆C的离心率，标准方程．（Ⅱ）设A（x1 ， y1），B（x2 ， y2），利用中点坐标公式以及平方差法求出AB的斜率，得到直线AB的方程，代入椭圆C的方程求出点的坐标，设F1R：y=k（x+1），联立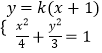 
，设P（x3 ， y3），Q（x4 ， y4），利用韦达定理，结合 
， 
，化简|PF1||QF1|，通过 
，求解|PF1||QF1|的取值范围．
