题目内容
 如图1,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF⊥平面ABCD,连接部分线段后围成一个空间几何体,如图2.
如图1,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF⊥平面ABCD,连接部分线段后围成一个空间几何体,如图2.(Ⅰ)求证:BE∥平面ADF;
(Ⅱ)求三棱锥F-BCE的体积.
分析:(Ⅰ)要求证:BE∥平面ADF,先在平面ADF中取DF中点为G,作出线段AG,证明BE∥AG即可.
(Ⅱ)求三棱锥F-BCE的体积,转化为VB-CEF即可;也可以直接解答,求底面面积和高;还可以求VE-CBF求底面面积和高,再求体积.
(Ⅱ)求三棱锥F-BCE的体积,转化为VB-CEF即可;也可以直接解答,求底面面积和高;还可以求VE-CBF求底面面积和高,再求体积.
解答: 证明:(Ⅰ)证法一:取DF中点为G,连接AG,EG中,
证明:(Ⅰ)证法一:取DF中点为G,连接AG,EG中,
CE=
DF,
∴EG∥CD
且EG=CD(2分)
又∵AB∥CD且AB=CD,
∴EG∥AB且EG=AB,四边形ABEG为平行四边形,
∴BE∥AG(4分)
∵BE?平面ADF,AG?平面ADF,
∴BE∥平面ADF,(6分)
证法二:由图1可知BC∥AD,CE∥DF,折叠之后平行关系不变.
∵BC?平面ADF,AD?平面ADF,
∴BC∥平面ADF,同理CE∥平面ADF(4分)
∵BC∩CE=C,BC,CE?平面BCE,∴平面BCE∥平面ADF.
∵BE?平面BCE,
∴BE∥平面ADF(6分)
 (Ⅱ)解法1:∵VF-BCE=VB-CEF,由图1可知BC⊥CD(8分)
(Ⅱ)解法1:∵VF-BCE=VB-CEF,由图1可知BC⊥CD(8分)
∵平面DCEF⊥平面ABCD,平面DCEF∩平面ABCD=CD,BC?平面ABCD,
∴BC⊥平面DCEF,(10分)
由图1可知DC=CE=1S△CEF=
CE×DC=
∴VF-BCE=VB-CEF=
×BC×S△CEF=
(12分)
解法2:由图可知CD⊥BC,CD⊥CE
∵BC∩CE=C,∴CD⊥平面BCE,
∵DF∥DC,点F到平面BCE的距离等于点D到平面BCE的距离为1,(8分)
由图1可知BC=CE=1S△BCE=
BC×CE=
∴VF-BCE=
×CD×S△BCE=
(12分)
解法3:过E作EH⊥FC,垂足为H
由图1可知BC⊥CD
∵平面DCEF⊥平面ABCD,
平面DCEF∩平面ABCD=CDBC?平面ABCD,
∴BC⊥平面DCEF,
∵EH?平面DCEF∴BC⊥EH,EH⊥平面BCF
由BC⊥FC,FC=
=
,S△BCF=
BC×DF=
,(10分)
在△CEF中,由等面积法可得EH=
,
∴VF-BCE=VE-BCF=
×EH×S△BCF=
(12分)
 证明:(Ⅰ)证法一:取DF中点为G,连接AG,EG中,
证明:(Ⅰ)证法一:取DF中点为G,连接AG,EG中,CE=
| 1 |
| 2 |
∴EG∥CD
且EG=CD(2分)
又∵AB∥CD且AB=CD,
∴EG∥AB且EG=AB,四边形ABEG为平行四边形,
∴BE∥AG(4分)
∵BE?平面ADF,AG?平面ADF,
∴BE∥平面ADF,(6分)
证法二:由图1可知BC∥AD,CE∥DF,折叠之后平行关系不变.
∵BC?平面ADF,AD?平面ADF,
∴BC∥平面ADF,同理CE∥平面ADF(4分)
∵BC∩CE=C,BC,CE?平面BCE,∴平面BCE∥平面ADF.
∵BE?平面BCE,
∴BE∥平面ADF(6分)
 (Ⅱ)解法1:∵VF-BCE=VB-CEF,由图1可知BC⊥CD(8分)
(Ⅱ)解法1:∵VF-BCE=VB-CEF,由图1可知BC⊥CD(8分)∵平面DCEF⊥平面ABCD,平面DCEF∩平面ABCD=CD,BC?平面ABCD,
∴BC⊥平面DCEF,(10分)
由图1可知DC=CE=1S△CEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴VF-BCE=VB-CEF=
| 1 |
| 3 |
| 1 |
| 6 |
解法2:由图可知CD⊥BC,CD⊥CE
∵BC∩CE=C,∴CD⊥平面BCE,
∵DF∥DC,点F到平面BCE的距离等于点D到平面BCE的距离为1,(8分)
由图1可知BC=CE=1S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
∴VF-BCE=
| 1 |
| 3 |
| 1 |
| 6 |
解法3:过E作EH⊥FC,垂足为H
由图1可知BC⊥CD
∵平面DCEF⊥平面ABCD,
平面DCEF∩平面ABCD=CDBC?平面ABCD,
∴BC⊥平面DCEF,
∵EH?平面DCEF∴BC⊥EH,EH⊥平面BCF
由BC⊥FC,FC=
| DC2+DF2 |
| 5 |
| 1 |
| 2 |
| ||
| 2 |
在△CEF中,由等面积法可得EH=
| 1 | ||
|
∴VF-BCE=VE-BCF=
| 1 |
| 3 |
| 1 |
| 6 |
点评:本题考查棱柱、棱锥的体积,考查转化思想,是中档题.

练习册系列答案
相关题目


 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.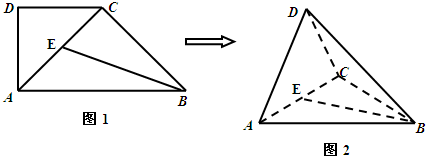 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;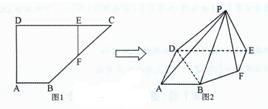 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.