题目内容
在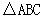 中,内角A,B,C所对的分别是a, b,c。已知a=2.c=
中,内角A,B,C所对的分别是a, b,c。已知a=2.c=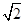 ,
, 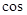 A=
A=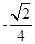 .
.
(I)求sin C和b的值;
(II)求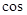 (2A+
(2A+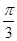 )的值.
)的值.
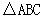 中,内角A,B,C所对的分别是a, b,c。已知a=2.c=
中,内角A,B,C所对的分别是a, b,c。已知a=2.c=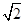 ,
, 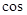 A=
A=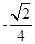 .
.(I)求sin C和b的值;
(II)求
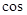 (2A+
(2A+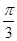 )的值.
)的值.(I) ,
, (II)
(II)
 ,
, (II)
(II)
试题分析:(Ⅰ)解:在
 中,由
中,由 可得
可得 .又由
.又由 及
及 可得
可得
由
 得
得 因为
因为 故解得
故解得
所以
 ,
,
(Ⅱ)解:由
 得
得 ,
,
所以,

点评:本题主要考查正弦定理和余弦定理的应用,二倍角公式以及两角和的余弦公式,同角三角函数
的基本关系的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, , 则
, 则 的值为 .
的值为 .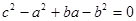 , 则角C的大小为( )
, 则角C的大小为( )



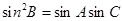 ;
;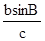 的值.
的值. ,则
,则




 为等边
为等边 所在平面内一点,满足
所在平面内一点,满足 ,若
,若 ,则
,则 的值为
的值为  中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, .则
.则 = .
= .