题目内容
【题目】已知函数
（1）判断
的奇偶性并证明；
（2）若
，求
的取值范围.[来
【答案】（1）奇函数（2）
【解析】
试题分析：（1）判断函数奇偶性首先判断函数定义域是否对称，再判断
的关系确定奇偶性；（2）将原函数式结合复合函数单调性判定方法可得到函数
单调性，进而可化简不等式
得到m的不等式，可求m得取值范围
试题解析：（1）判断：f（x）为奇函数，-----------------------1分
证明如下：
因为，定义域为
关于原点对称---------------------3分
-----------------6分
（2）
为上的减函数，--------------------8分
由复合函数的单调性可知f（x）在定义域上是减函数，---------------9分
所以有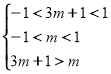
解得：------------------12分
练习册系列答案
相关题目
