题目内容
对于函数 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;②
;② ,
, ;③
;③ ,
, ;④
;④
 ,
, ,则在区间
,则在区间 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
A.①② B.③④ C.②③ D.①④
【答案】
D.
【解析】
试题分析:对于①,由 得
得 ,即为唯一的“友好点”;对于②,
,即为唯一的“友好点”;对于②, 无解,故不存在“友好点”;对于③,
无解,故不存在“友好点”;对于③, ,而
,而 是
是 上的减函数,且
上的减函数,且 ,故
,故 与
与 在区间
在区间 上有无穷多个“友好点”;对于④,
上有无穷多个“友好点”;对于④, 时,
时, .令
.令 当
当 时,
时, ;当
;当 时,
时, .
. 在
在 上是增函数,在
上是增函数,在 上是减函数,
上是减函数, 在
在 处取最大值,且
处取最大值,且 ,从而在
,从而在 上,
上, 恒成立,
恒成立, 在
在 上是减函数,在
上是减函数,在 上是增函数,
上是增函数, 在
在 处取最小值,且
处取最小值,且 ,即
,即 与
与 有唯一的“友好点”.综上所述选D.
有唯一的“友好点”.综上所述选D.
考点:1.新定义“友好点”;2.函数的单调性、最值.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 ,
, ;
; ,
, ;
; ,
, ;
;
 ,
, ,
,  上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( ) 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 ,
, ②
② ,
,
 ,
, ④
④ ,
,
 上存在“友好点”的有( )
上存在“友好点”的有( )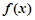 与
与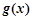 和区间E,如果存在
和区间E,如果存在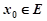 ,使
,使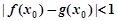 ,则我们称函数
,则我们称函数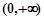 上“互相接近”的是( )
上“互相接近”的是( ) 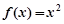 ,
,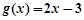 B.
B.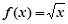 ,
,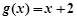
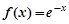 ,
,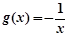 D.
D.
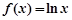 ,
,