题目内容
(本小题满分14分)
设函数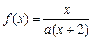 ,方程
,方程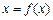 有唯一解,其中实数
有唯一解,其中实数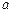 为常数,
为常数,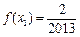 ,
,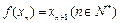
(1)求 的表达式;
的表达式;
(2)求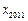 的值;
的值;
(3)若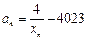 且
且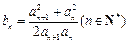 ,求证:
,求证: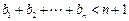
设函数
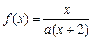 ,方程
,方程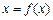 有唯一解,其中实数
有唯一解,其中实数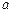 为常数,
为常数,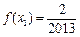 ,
,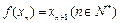
(1)求
 的表达式;
的表达式;(2)求
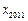 的值;
的值;(3)若
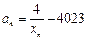 且
且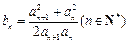 ,求证:
,求证: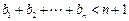
解:(1)由 ,可化简为
,可化简为
 -------2分
-------2分 当且仅当
当且仅当 时,方程
时,方程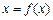 有唯一解. ---3分
有唯一解. ---3分
从而 -------4分
-------4分
(2)由已知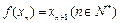 ,得
,得 -------5分
-------5分
 ,即
,即
 数列
数列 是以
是以 为首项,
为首项, 为公差的等差数列. -------6分
为公差的等差数列. -------6分
 ,
,
 ,
, ,即
,即

 -------7分
-------7分
故 -------8分
-------8分
(3)证明: ,
, -------10分
-------10分
 ---12分
---12分
 --13分
--13分
故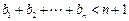 -------14分
-------14分
 ,可化简为
,可化简为
 -------2分
-------2分 当且仅当
当且仅当 时,方程
时,方程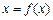 有唯一解. ---3分
有唯一解. ---3分从而
 -------4分
-------4分(2)由已知
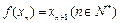 ,得
,得 -------5分
-------5分 ,即
,即
 数列
数列 是以
是以 为首项,
为首项, 为公差的等差数列. -------6分
为公差的等差数列. -------6分 ,
,
 ,
, ,即
,即

 -------7分
-------7分故
 -------8分
-------8分(3)证明:
 ,
, -------10分
-------10分 ---12分
---12分 --13分
--13分故
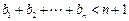 -------14分
-------14分略

练习册系列答案
相关题目
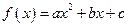
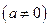 满足
满足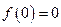 ,对于任意
,对于任意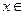 R都有
R都有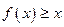 ,且
,且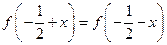 ,令
,令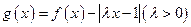 .
.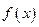 的表达式;
的表达式;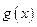 的单调区间;
的单调区间;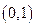 上的零点个数.
上的零点个数.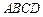 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线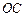 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段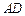 的中点
的中点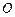 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线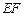 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.
 ,则满足“若
,则满足“若 ,则
,则 ”的函数
”的函数 的个数为*u
的个数为*u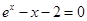 的一个根所在的区间为
的一个根所在的区间为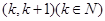 ,则k的值为( )
,则k的值为( )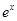

 该产品销售量(亦即该产品的年产量)
该产品销售量(亦即该产品的年产量)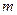 万件
万件 与年促销费用
与年促销费用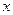 万元(
万元(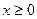 )满足
)满足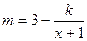 (
(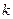 为常数).已知2011年生产该产品的前期投入需要8万元,每生产1万件该产品需要再投入16万元,企业将每件该产品的销售价格定为每件产品年平均成本的1.5倍(定价不考虑促销成本).
为常数).已知2011年生产该产品的前期投入需要8万元,每生产1万件该产品需要再投入16万元,企业将每件该产品的销售价格定为每件产品年平均成本的1.5倍(定价不考虑促销成本). 促销费用最少是多少?
促销费用最少是多少?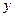 (万元)表示为年促销费用
(万元)表示为年促销费用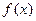 是定义在
是定义在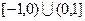 上的奇函数,当
上的奇函数,当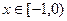 时,
时,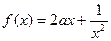 (a为实数).
(a为实数).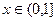 时,求
时,求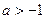 时,试判断
时,试判断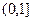 上的单调性,并证明你的结论.
上的单调性,并证明你的结论. )(2,3)
)(2,3)