题目内容
平面向量 ,则这样的向量
,则这样的向量 有
有
- A.1个
- B.2个
- C.多个2个
- D.不存在
A
分析:由题意可得: ,再由点到直线的距离公式可得:
,再由点到直线的距离公式可得: =r,可得直线与圆相切,即直线与圆只有一个交点,进而得到答案.
=r,可得直线与圆相切,即直线与圆只有一个交点,进而得到答案.
解答:因为 ,并且
,并且 ,
,
所以 ,
,
所以由点到直线的距离公式可得: =r,
=r,
所以直线与圆相切,即直线与圆只有一个交点,
所以向量 有1个.
有1个.
故选A.
点评:解决此类问题的关键是熟练掌握向量的数量积运算,以及直线与圆的位置关系,本题考查了点到直线的距离公式,此题属于中档题.
分析:由题意可得:
 ,再由点到直线的距离公式可得:
,再由点到直线的距离公式可得: =r,可得直线与圆相切,即直线与圆只有一个交点,进而得到答案.
=r,可得直线与圆相切,即直线与圆只有一个交点,进而得到答案.解答:因为
 ,并且
,并且 ,
,所以
 ,
,所以由点到直线的距离公式可得:
 =r,
=r,所以直线与圆相切,即直线与圆只有一个交点,
所以向量
 有1个.
有1个.故选A.
点评:解决此类问题的关键是熟练掌握向量的数量积运算,以及直线与圆的位置关系,本题考查了点到直线的距离公式,此题属于中档题.

练习册系列答案
相关题目
 (
( ,
, 分别为与x轴,y轴正方向相同的单位向量),则点P的斜坐标为(x,y),则以O为圆心,1为半径的圆在斜坐标系下方程为
分别为与x轴,y轴正方向相同的单位向量),则点P的斜坐标为(x,y),则以O为圆心,1为半径的圆在斜坐标系下方程为




 和
和 为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量 +μ
+μ 和
和 表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中< ,
, 和
和 为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量 ,则存在唯一的一对实数λ,μ,使得
,则存在唯一的一对实数λ,μ,使得 =
= +μ
+μ ,我们就把实数对(λ,μ)称作向量
,我们就把实数对(λ,μ)称作向量 的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用
的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用 和
和 表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<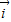 ,
, >=
>= ,
,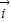 和
和 做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量 的坐标;
的坐标;