题目内容
16.已知有条光线从点A(-2,1)出发射向x轴B,经过x轴反射后射向y轴上的C点,再经过y轴反射后到达点D(-2,7).(1)求直线BC的方程.
(2)求光线从A点到达D点所经过的路程.
分析 (1)由题意画出图形,找出A关于x轴的对称点,D关于y轴的对称点,由直线方程的两点式求得直线BC的方程;
(2)直接由两点间的距离公式得答案.
解答 解:如图,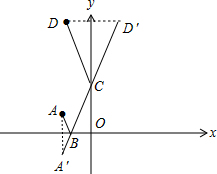
(1)∵A(-2,1),
∴A点关于x轴的对称点为A′(-2,-1),
∵D(-2,7),
∴D点关于y轴的对称点D′(2,7).
由对称性可得,A′、D′所在直线方程即为BC所在直线方程,
∴BC:$\frac{y+1}{7+1}=\frac{x+2}{2+2}$,整理得2x-y+3=0;
(2)由图可得,光线从A点到达D点所经过的路程即为|A′D′|=$\sqrt{(-2-2)^{2}+(-1-7)^{2}}=4\sqrt{5}$.
点评 本题考查点关于直线的对称点的求法,考查了数学转化思想方法,是中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.椭圆的四个顶点A,B,C,D构成四边形为菱形,若菱形ABCD的内切圆恰好过焦点,则椭圆离心率为( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | $\frac{3+\sqrt{5}}{8}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
4.已知集合A={x|x2-4=0},B={1,2},则A∩B=( )
| A. | 2 | B. | {-2,2} | C. | {2} | D. | ∅ |
1.已知抛物线y=ax2+bx+c通过点P(1,1),且在点Q(2,-1)处的切线平行于直线y=x-3,则抛物线方程为( )
| A. | y=3x2-11x+9 | B. | y=3x2+11x+9 | C. | y=3x2-11x-9 | D. | y=-3x2-11x+9 |
8.若直线(1+a)x+y+1=0与圆(x-1)2+y2=1相切,则a的值为( )
| A. | 1,-1 | B. | 2,-2 | C. | 1 | D. | -1 |