题目内容
已知![]() 是矩形,
是矩形,![]() ,
,![]() 分别是线段
分别是线段![]() 的中点,
的中点,![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)在棱![]() 上找一点
上找一点![]() ,使
,使![]() ∥平面
∥平面![]() ,并说明理由.
,并说明理由.
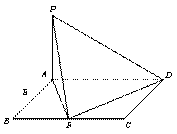
【解】:证明:在矩形ABCD中,因为AD=2AB,点F是BC的中点,所以∠AFB=∠DFC=45°.
所以∠AFD=90°,即AF⊥FD. ……………………4分
又PA⊥平面ABCD,所以PA⊥FD.所以FD⊥平面PAF. ……………………6分
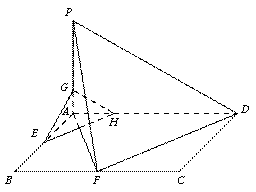 (Ⅱ)过E作EH//FD交AD于H,
(Ⅱ)过E作EH//FD交AD于H,
则EH//平面PFD,且 AH =![]() AD.
AD.
再过H作HG//PD交PA于G, ……………………9分
所以GH//平面PFD,且 AG=![]() PA.
PA.
所以平面EHG//平面PFD. ……………………11分
所以EG//平面PFD.
从而点G满足AG=![]() PA.
PA.

练习册系列答案
相关题目

 (2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD.
(2013•内江二模)已知ABCD是矩形,AD=4,AB=2,E、F分别是AB、BC 的中点,PA丄面ABCD. 的底面
的底面 是矩形,
是矩形, 、
、 分别是
分别是 、
、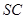 的中点,
的中点,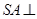 底面
底面 ,
,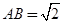
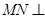 平面
平面
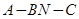 的余弦值
的余弦值
 的底面
的底面 是矩形,
是矩形, 、
、 分别是
分别是 、
、 的中点,
的中点, 底面
底面 ,
,
 平面
平面
 的余弦值
的余弦值