如图.已知矩形ABCD.M.N分别是AD.BC的中点.且AM=AB.将矩形沿MN折成直二面角.若P是DN上一动点.求P到BM距离的最小值．题目和参考答案——青夏教育精英家教网—

题目内容

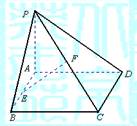
如图，已知矩形ABCD，M、N分别是AD、BC的中点，且AM=AB，将矩形沿MN折成直二面角，若P是DN上一动点，求P到BM距离的最小值．

分析：利用正方体模型，P是DN上一动点，要求P到BM距离的最小值，即求DN与BM的距离，从而转化为平面BFM与平面EDN的距离

解答：解：由题意，半平面可以看作正方体ABEF-MNCD的两个相邻的面，连接FB，FM，EN，DN，
则平面BFM∥平面EDN
P是DN上一动点，要求P到BM距离的最小值，即求DN与BM的距离，从而转化为平面BFM与平面EDN的距离
连接AC，则AC⊥平面BFM，AC⊥平面EDN，且垂足分AC三等分
∴平面BFM与平面EDN的距离为

点评：本题以平面图形的翻折为载体，考查点线距离，线线距离，面面距离，关键是等价转化．

练习册系列答案

相关题目

如图，已知在矩形ABCD中，AB=3，BC=4，沿对角线AC将△ABC折起，使B点在平面ADC内的射影恰好落在AD上，求：

(1)异面直线AB与CD成的角；

(2)异面直线AB与CD的距离；

(3)二面角B－AC－D的大小．

如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、

PC的中点．

（1）求证：EF∥平面PAD；

（2）求证：EF⊥CD；

（3）若ÐPDA＝45°求EF与平面ABCD所成的角的大小．

【解析】本试题主要考查了线面平行和线线垂直的运用，以及线面角的求解的综合运用

第一问中，利用连AC，设AC中点为O，连OF、OE在△PAC中，∵ F、O分别为PC、AC的中点 ∴ FO∥PA …………①在△ABC中，∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD∵ EF Ì 平面EFO ∴ EF∥平面PAD．

第二问中在矩形ABCD中，∵ EO∥BC，BC⊥CD ∴ EO⊥CD 又 ∵ FO∥PA，PA⊥平面AC ∴ FO⊥平面AC∴ EO为EF在平面AC内的射影 ∴ CD⊥EF．

第三问中，若ÐPDA＝45°，则 PA＝AD＝BC ∵ EOBC，FOPA

∴ FO＝EO 又∵ FO⊥平面AC∴ △FOE是直角三角形 ∴ ÐFEO＝45°

证：连AC，设AC中点为O，连OF、OE（1）在△PAC中，∵ F、O分别为PC、AC的中点∴ FO∥PA …………① 在△ABC中，∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD

∵ EF Ì 平面EFO ∴ EF∥平面PAD．

（2）在矩形ABCD中，∵ EO∥BC，BC⊥CD∴ EO⊥CD 又 ∵ FO∥PA，PA⊥平面AC ∴ FO⊥平面AC ∴ EO为EF在平面AC内的射影 ∴ CD⊥EF．

（3）若ÐPDA＝45°，则 PA＝AD＝BC ∵ EOBC，FOPA

∴ FO＝EO 又 ∵ FO⊥平面AC ∴ △FOE是直角三角形 ∴ ÐFEO＝45°

在A、B、C、D四小题中只能选做2题，每小题10，共计20分。请在答题卡指定区域作答。解答应写出文字说明、证明过程或演算步骤。

A、选修4-1：几何证明选讲

如图，已知梯形ABCD为圆内接四边形，AD//BC，过C作该圆的切线，交AD的延长线于E，求证：ΔABC∽ΔEDC。

B、选修4-2：矩形与变换

已知为矩阵属于λ的一个特征向量，求实数a，λ的值及A2。

C、选修4-4：坐标系与参数方程

在平面直角坐标系xoy中，曲线C的参数方程为（α为参数），曲线D的参数方程为，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。

D、选修4-5：不等式选讲

已知a，b都是正实数，且ab=2。求证：（1+2a）（1+b）≥9。

如图，已知几何体ABC-DEF中，△ABC及△DEF都是边长为2的等边三角形，四边形ABEF为矩形，且CD=AF+2，CD//AF，O为AB中点.

（1）求证：AB⊥平面DCO

（2）若M为CD中点，AF=x，则当x取何值时，使AM与平面ABEF所成角为45°？

试求相应的x值的.

（3）求该几何体在(2)的条件下的体积.

在A、B、C、D四小题中只能选做2题，每小题10，共计20分。请在答题卡指定区域作答。解答应写出文字说明、证明过程或演算步骤。
A、选修4-1：几何证明选讲
如图，已知梯形ABCD为圆内接四边形，AD//BC，过C作该圆的切线，交AD的延长线于E，求证：ΔABC∽ΔEDC。

B、选修4-2：矩形与变换
已知为矩阵属于λ的一个特征向量，求实数a，λ的值及A2。
C、选修4-4：坐标系与参数方程
在平面直角坐标系xoy中，曲线C的参数方程为（α为参数），曲线D的参数方程为，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。
D、选修4-5：不等式选讲
已知a，b都是正实数，且ab=2。求证：（1+2a）（1+b）≥9。

试题分类