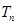题目内容
((本小题14分)
已知函数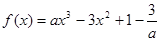
(I)若函数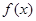 在
在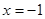 时取得极值,求实数
时取得极值,求实数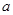 的值;
的值;
(II)试讨论函数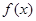 的单调性;
的单调性;

【答案】
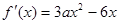 (
(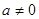 )
……………………………1分
)
……………………………1分
(I)∵函数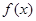 在
在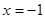 时取到极值
时取到极值
∴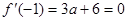 解得
解得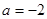
经检验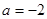 函数
函数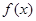 在
在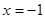 时取到极小值(不检验扣1分)
时取到极小值(不检验扣1分)
∴实数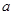 的值-2
…………………………4分
的值-2
…………………………4分
(II)由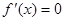 得
得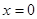 或
或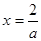 …………………………5分
…………………………5分
①当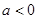 时,
时,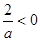
由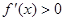 得
得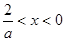
由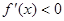 得
得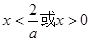
∴函数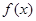 得单调增区间为
得单调增区间为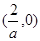 ,单调减区间为
,单调减区间为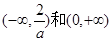 …………7分
…………7分
②当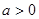 时,
时, ,同理可得函数
,同理可得函数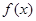 得单调增区间为
得单调增区间为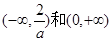 ,
,
单调减区间为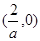 ………………………………9分
………………………………9分
(II)假设存在满足要求的两点A,B,即在点A、B处的切线都与y轴垂直,则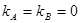
即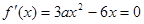 解得
解得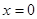 或
或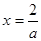
∴A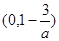 ,B
,B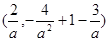

【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以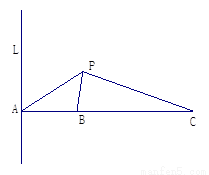
 km,用
km,用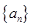 中,
中,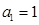 ,前
,前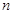 项和
项和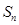 满足条件
满足条件 ,
,
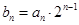 ,求数列
,求数列 的前
的前