题目内容
(本小题12分)已知:以点C (t, 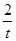 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与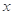 轴交于点O, A,
轴交于点O, A,
与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若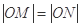 ,求圆C的方程.
,求圆C的方程.
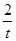 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与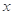 轴交于点O, A,
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若
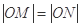 ,求圆C的方程.
,求圆C的方程.(1)根据条件写成圆的方程,求出点A,B的坐标,进而写出△OAB的面积即可得证;
(2)
(2)

试题分析:(1)
 ,
, .
.设圆
 的方程是
的方程是  ,
,令
 ,得
,得 ;令
;令 ,得
,得 ,
, ,即:
,即: 的面积为定值.……………6分
的面积为定值.……………6分(2)

 垂直平分线段
垂直平分线段 .
. ,
, 直线
直线 的方程是
的方程是 .
. ,解得:
,解得: ,
, 当
 时,圆心
时,圆心 的坐标为
的坐标为 ,
, ,
,此时
 到直线
到直线 的距离
的距离 ,
,圆C与直线
 相交于两点,
相交于两点,当
 时,圆心C的坐标为
时,圆心C的坐标为 ,此时C 到直线
,此时C 到直线 的距离
的距离 ,
,圆C与直线
 相交,所以
相交,所以 不符合题意舍去.
不符合题意舍去.所以圆C的方程为
 ……12分
……12分点评:解决直线与圆的位置关系题目时,要注意使用几何法,即考查圆心到直线的距离与半径之间的关系,这样比联立方程组简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 过坐标原点,则圆心C到直线
过坐标原点,则圆心C到直线 距离的最小值等于 .
距离的最小值等于 . 满足
满足 ,那么
,那么 的最小值为 .
的最小值为 . :
:
 为参数),圆
为参数),圆 (极轴与
(极轴与 轴的非负半轴重合,且单位长度相同)。
轴的非负半轴重合,且单位长度相同)。 到直线
到直线 ,求
,求 的值。
的值。 与曲线
与曲线 有公共点,则b的取值范围为 。
有公共点,则b的取值范围为 。 上的圆的方程是( )
上的圆的方程是( )



 ,圆心在直线
,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求圆C的方程
,求圆C的方程 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆 相交于
相交于 两点,
两点, 是
是 的中点.
的中点.
 时,求直线
时,求直线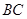 是圆
是圆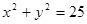 的动弦,且
的动弦,且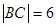 ,则
,则