题目内容
（2012•山东）圆（x+2）2+y2=4与圆（x-2）2+（y-1）2=9的位置关系为（ ）
分析：求出两圆的圆心和半径，计算两圆的圆心距，将圆心距和两圆的半径之和或半径之差作对比，判断两圆的位置关系．
解答：解：圆（x+2）2+y2=4的圆心C1（-2，0），半径r=2．
圆（x-2）2+（y-1）2=9的圆心C2（2，1），半径R=3，
两圆的圆心距d=
=
，
R+r=5，R-r=1，
R+r＞d＞R-r，
所以两圆相交，
故选B．
圆（x-2）2+（y-1）2=9的圆心C2（2，1），半径R=3，
两圆的圆心距d=
| (-2-2)2+ (0-1)2 |
| 17 |
R+r=5，R-r=1，
R+r＞d＞R-r，
所以两圆相交，
故选B．
点评：本题考查圆与圆的位置关系及其判定的方法，关键是求圆心距和两圆的半径．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
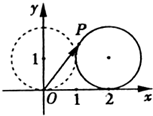（2012•山东）如图，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在（0，1），此时圆上一点P的位置在（0，0），圆在x轴上沿正向滚动．当圆滚动到圆心位于（2，1）时，
中，
是抛物线
的焦点，
是抛物线
上
三点的圆的圆心为
，点
．
与抛物线
若存在，求出点
，直线
与抛物线
，
与
，求当
时，
的最小值．