题目内容
已知函数,f(x)=alnx﹣ax﹣3(a∈R).
(1 )当a=1时,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,问:m在什么范围取值时,对于任意的t∈[1,2],函数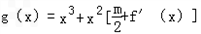 在区间(t,3)上总存在极值?
在区间(t,3)上总存在极值?
(1 )当a=1时,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,问:m在什么范围取值时,对于任意的t∈[1,2],函数
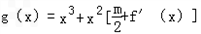 在区间(t,3)上总存在极值?
在区间(t,3)上总存在极值?解:(1) 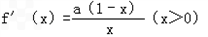 ,
,
当a=1时,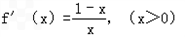
令导数大于0,可解得0<x<1,
令导数小于0,可解得x<0(舍)或x>1
故函数的单调增区间为(0,1),单调减区间是(1,+∞)
(2)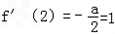 得a=﹣2,f(x)=﹣2lnx+2x﹣3
得a=﹣2,f(x)=﹣2lnx+2x﹣3
∴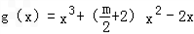 ,
,
∴g'(x)=3x2+(m+4)x﹣2
∵g(x)在区间(t,3)上总不是单调函数,且g'(0)=﹣2
∴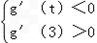 ,
,
由题意知:对于任意的t∈[1,2],g'(t)<0恒成立,
所以有: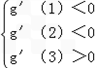 ,
,
∴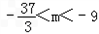 .
.
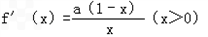 ,
,当a=1时,
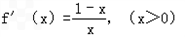
令导数大于0,可解得0<x<1,
令导数小于0,可解得x<0(舍)或x>1
故函数的单调增区间为(0,1),单调减区间是(1,+∞)
(2)
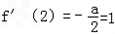 得a=﹣2,f(x)=﹣2lnx+2x﹣3
得a=﹣2,f(x)=﹣2lnx+2x﹣3∴
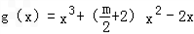 ,
,∴g'(x)=3x2+(m+4)x﹣2
∵g(x)在区间(t,3)上总不是单调函数,且g'(0)=﹣2
∴
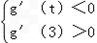 ,
,由题意知:对于任意的t∈[1,2],g'(t)<0恒成立,
所以有:
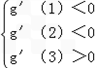 ,
,∴
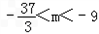 .
.
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
