题目内容

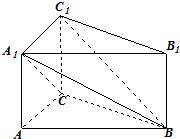精英家教网在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC⊥BC，且AB=4，AC=AA1=2．求二面角C1-A1B-C的余弦值．
分析：由题意由于已知图象中出现了两两垂直的直线并且还已知了各边的长度，所以选择利用空间向量的方法求解二面角即可．
解答：精英家教网解：建立如图直角坐标系，
则A1(2，0，2)，B(0，2
3
，0)，B1(0，2
3
，2)，
易知，平面A1BC的一个法向量
m
=(1，0，-1)．
设平面A1BC1的一个法向量为
n
=(x，y，z)，
由
n
•
C1A1
=0
n
•
C1B
=0
，得
n
=(0，1，
3
)．
cos＜
m
，
n
＞=
m
•
n
|
m
|•|
n
|
=-
6
4
，
所以二面角C1-A1B-C的余弦值是
6
4
．
点评：此题中点考查了学生利用空间向量求解二面角，此法的关键是要找准两平面的法向量夹角与二面角的大小的关系．
练习册系列答案
相关题目
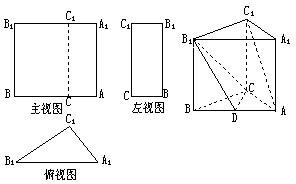精英家教网已知三棱柱ABC-A1B1C1的三视图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，cos∠A1=
35
．
（1）在三棱柱ABC-A1B1C1中，求证：BC⊥AC1；
（2）在三棱柱ABC-A1B1C1中，若D是底边AB的中点，求证：AC1∥平面CDB1．
（3）若三棱柱的高为5，求三视图中左视图的面积．
精英家教网如图：在正三棱柱ABC-A1 B1 C1中，AB=
AA13
=a，E，F分别是BB1，CC1上的点且BE=a，CF=2a．
（Ⅰ）求证：面AEF⊥面ACF；
（Ⅱ）求三棱锥A1-AEF的体积．
在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
5
，BC=4，在A1在底面ABC的投影是线段BC的中点O．
（1）求点C到平面A1ABB1的距离；
（2）求二面角A-BC1-B1的余弦值；
（3）若M，N分别为直线AA1，B1C上动点，求MN的最小值．
（2012•江西）在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
5
，BC=4，在A1在底面ABC的投影是线段BC的中点O．
（1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；
（2）求平面A1B1C与平面BB1C1C夹角的余弦值．
（2013•北京）如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1-BC1-B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求
BDBC1
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网