题目内容
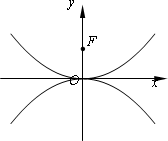
 设抛物线C1:x2=4y的焦点为F,曲线C2与C1关于原点对称.
设抛物线C1:x2=4y的焦点为F,曲线C2与C1关于原点对称.(Ⅰ) 求曲线C2的方程;
(Ⅱ) 曲线C2上是否存在一点P(异于原点),过点P作C1的两条切线PA,PB,切点A,B,满足|AB|是|FA|与|FB|的等差中项?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(Ⅰ)根据曲线C2与C1关于原点对称,可求曲线C2的方程;
(Ⅱ)求出切线PA、PB的方程,可得直线AB的方程,代入抛物线方程,求出|AB|,利用抛物线定义,结合|FA|+|FB|=2|AB|,即可得出结论.
(Ⅱ)求出切线PA、PB的方程,可得直线AB的方程,代入抛物线方程,求出|AB|,利用抛物线定义,结合|FA|+|FB|=2|AB|,即可得出结论.
解答:(Ⅰ)解;因为抛物线C1:x2=4y的焦点为F,曲线C2与C1关于原点对称,所以C2方程为x2=-4y.
(Ⅱ)解:设P(x0,-
),A(x1,y1),B(x2,y2)(x1≠x2).
y=
x2的导数为y′=
x,则切线PA的方程y-y1=
x1(x-x1),
又y1=
x12,得y=
x1x-y1,
因点P在切线PA上,故-
x02=
x1x0-y1.
同理-
x02=
x2x0-y2.
所以直线-
x02=
x0x-y经过A,B两点,
即直线AB方程为-
x02=
x0x-y,即y=
x0x+
x02,
代入x2=4y得x2-2x0x-x02=0,则x1+x2=2x0,x1x2=-x02,
所以|AB|=
•
=
,
由抛物线定义得|FA|=y1+1,|FB|=y2+1.
所以|FA|+|FB|=(y1+y2)+2=
x0(x1+x2)+
x02+2,
由题设知,|FA|+|FB|=2|AB|,即(
x02+2)2=4x02(8+2x02),
解得x02=
,从而y0=
.
综上,存在点P满足题意,点P的坐标为(
,
)或(-
,
).
(Ⅱ)解:设P(x0,-
| x02 |
| 4 |
y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
又y1=
| 1 |
| 4 |
| 1 |
| 2 |
因点P在切线PA上,故-
| 1 |
| 4 |
| 1 |
| 2 |
同理-
| 1 |
| 4 |
| 1 |
| 2 |
所以直线-
| 1 |
| 4 |
| 1 |
| 2 |
即直线AB方程为-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
代入x2=4y得x2-2x0x-x02=0,则x1+x2=2x0,x1x2=-x02,
所以|AB|=
1+
|
| (x1+x2)2-4x1x2 |
| (8+2x02)•x02 |
由抛物线定义得|FA|=y1+1,|FB|=y2+1.
所以|FA|+|FB|=(y1+y2)+2=
| 1 |
| 2 |
| 1 |
| 2 |
由题设知,|FA|+|FB|=2|AB|,即(
| 3 |
| 2 |
解得x02=
32
| ||
| 23 |
13-8
| ||
| 23 |
综上,存在点P满足题意,点P的坐标为(
2
| ||||
| 23 |
13-8
| ||
| 23 |
2
| ||||
| 23 |
13-8
| ||
| 23 |
点评:本题主要考查抛物线几何性质,直线与抛物线的位置关系、等差中项等基础知识,同时考查解析几何的基本思想方法和运算求解能力,属于中档题.

练习册系列答案
相关题目
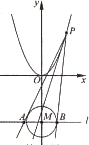 如图,设P是抛物线C1:x2=y上的动点.过点P做圆C2:x2+(y+3)2=1的两条切线,交直线l:y=-3于A,B两点.
如图,设P是抛物线C1:x2=y上的动点.过点P做圆C2:x2+(y+3)2=1的两条切线,交直线l:y=-3于A,B两点. 已知点D(0,-2),过点D作抛物线C1:x2=2py(p>0)的切线l,切点A在第二象限,如图
已知点D(0,-2),过点D作抛物线C1:x2=2py(p>0)的切线l,切点A在第二象限,如图