题目内容
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少
(本题可以参考两个分类变量x和y有关系的可信度表:)
(1)
(2)出错的概率为0.001 患色盲 不患色盲 总计 男 38 442 480 女 6 514 520 总计 44 956 1000
解析试题分析:解:(1)
(2)假设H :“性别与患色盲没有关系”先算出K 的观测值: 患色盲 不患色盲 总计 男 38 442 480 女 6 514 520 总计 44 956 1000 
则有
即是H 成立的概率不超过0.001,
若认为“性别与患色盲有关系”,则出错的概率为0.001
考点:独立性检验
点评:主要是考查了独立性检验的思想的运用,属于基础题。

练习册系列答案
相关题目
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x
的线性回归方程
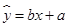 ;
; (Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理
想?
(参考公式:
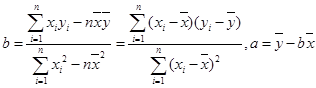 )
) 对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如下表:
| 寿命(h) | 频率 |
| 500600 | 0.10 |
| 600700 | 0.15 |
| 700800 | 0.40 |
| 800900 | 0.20 |
| 9001000 | 0.15 |
| 合计 | 1 |
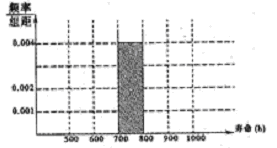
(I)在下图中补齐频率分布直方图;
(II)估计元件寿命在500800h以内的概率。
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
| | 患病 | 未患病 | 总计 |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
 P(Y=0).
P(Y=0).(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次, 若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为
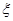 .,求
.,求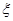 的期望E(
的期望E(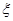 )和方差D(
)和方差D(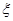 ).
).参考公式:
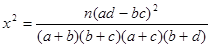 (其中
(其中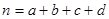 )
)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
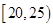 ,第2组
,第2组 ,第3组
,第3组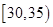 ,第4组
,第4组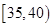 ,第5组
,第5组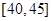 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
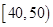 ,
,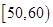 ,
,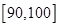 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.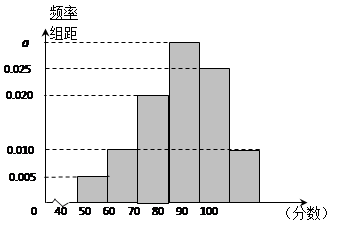
 的值;
的值;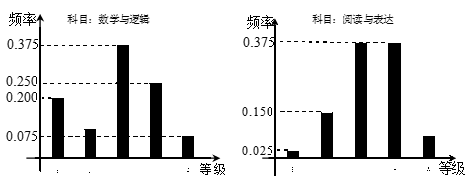
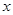 与销售额
与销售额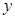 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: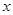 与销售额
与销售额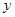 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: