题目内容
20.已知函数f(x)是偶函数,且f(x)在[0,+∞)上的解析式是f(x)=2x+1,则f(x)在(-∞,0)上的解析式为f(x)=-2x+1.分析 利用函数是偶函数,f(-x)=f(x),f(x)在[0,+∞)上的解析式是f(x)=2x+1,当x<0时,则-x>0,可求f(x)在(-∞,0)上的解析式.
解答 解:由题意,函数是偶函数,f(-x)=f(x),
当x≥0时,f(x)=2x+1,
那么:f(-x)=-2x+1=f(x),
∴f(x)=-2x+1,
故答案为:f(x)=-2x+1.
点评 本题考了函数解析式的求法,利用了函数是偶函数的性质求解.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知x0是函数f(x)=3x+$\frac{2}{1-x}$的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)<0 | D. | f(x1)>0,f(x2)>0 |
11.下列刻画一组数据离散程度的是( )
| A. | 平均数 | B. | 方差 | C. | 中位数 | D. | 众数 |
15.2011年4月 25日,全国人大常委会公布《中华人民共和国个人所得税法修正案(草案)》,向社会公开征集意见.草案规定,公民全月工薪不超过3000元的部分不必纳税,超过3000元的部分为全月应纳税所得额.此项税款按下表分段累进计算.
依据草案规定,解答下列问题:
(1)李工程师的月工薪为8000元,则他每月应当纳税多少元?
(2)若某纳税人的月工薪不超过10000元,他每月的纳税金额能超过月工薪的8%吗?若能,请给出该纳税人的月工薪范围;若不能,请说明理由.
| 级 数 | 全月应纳税所得额 | 税 率 |
| 1 | 不超过 1500元的部分 | 5% |
| 2 | 超过 1500元至4500元的部分 | 10% |
| 3 | 超过 4500元至9000元的部分 | 20% |
(1)李工程师的月工薪为8000元,则他每月应当纳税多少元?
(2)若某纳税人的月工薪不超过10000元,他每月的纳税金额能超过月工薪的8%吗?若能,请给出该纳税人的月工薪范围;若不能,请说明理由.
20.已知平面区域Ω:$\left\{{\begin{array}{l}{3x+4y-18≤0}\\{x≥2}\\{y≥0}\end{array}}$,夹在两条斜率为-$\frac{3}{4}$的平行直线之间,且这两条平行直线间的最短距离为m.若点P(x,y)∈Ω,且mx-y的最小值为p,$\frac{y}{x+m}$的最大值为q,则pq等于( )
| A. | $\frac{27}{22}$ | B. | $\frac{2}{5}$ | C. | $\frac{27}{25}$ | D. | 0 |
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=$\sqrt{3}$,E为线段PD上一点,记$\frac{PE}{PD}$=λ. 当λ=$\frac{1}{2}$时,二面角D-AE-C的平面角的余弦值为$\frac{2}{3}$.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=$\sqrt{3}$,E为线段PD上一点,记$\frac{PE}{PD}$=λ. 当λ=$\frac{1}{2}$时,二面角D-AE-C的平面角的余弦值为$\frac{2}{3}$.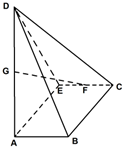 已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分别为AD,CE的中点,其中二面角D-AE-C的平面角的正切值为-tan2.
已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分别为AD,CE的中点,其中二面角D-AE-C的平面角的正切值为-tan2.