题目内容
已知-7,a1,a2,-1四个实数成等差数列,-4,b1,b2,b3,-1五个实数成等比数列,则 = ( )
= ( )
| A.1 | B.-1 | C.2 | D.±1 |
B
解析试题分析:根据等差数列的定义,我们可以确定a2-a1=-2,利用等比数列的定义,可以得出b2=-4,故可以求出 .根据-7,a1,a2,-1四个实数成等差数列,公差为2,-4,b1,b2,b3,-1五个实数成等比数列,公比为
.根据-7,a1,a2,-1四个实数成等差数列,公差为2,-4,b1,b2,b3,-1五个实数成等比数列,公比为 ,b=-
,b=- ,故可知
,故可知 =-1,故答案为B.
=-1,故答案为B.
考点:等差数列、等比数列
点评:本题考查等差数列、等比数列的定义,考查学生的计算能力,求b2时,容易错误得出两个解,需要谨慎判断.

练习册系列答案
相关题目
已知数列{ }中,
}中, =
= ,
, +
+ (n
(n ,则数列{
,则数列{ }的通项公式为( )
}的通项公式为( )
A. | B. |
C. | D. |
已知函数 的图象与直线
的图象与直线 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为 ,则
,则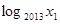 +
+ +…+
+…+ 的值为( )
的值为( )
| A.-1 | B.1-log20132012 | C.-log20132012 | D.1 |
在函数y=f(x)的图象上有点列(xn,yn),若数列{xn}是等差数列,数列{yn}是等比数列,则函数y=f(x)的解析式可能为( )
| A.f(x)=2x+1 | B.f(x)=4x2 |
| C.f(x)=log3x | D.f(x)= x x |
数列 的前
的前 项和为
项和为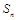 ,若
,若 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知等比数列 中,公比
中,公比 若
若 则
则 有( )
有( )
| A.最小值-4 | B.最大值-4 | C.最小值12 | D.最大值12 |
1202年,意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系: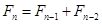 (
( ),其中
),其中 表示第
表示第 个月的兔子的总对数,
个月的兔子的总对数, ,则
,则 的值为( )
的值为( )
| A.13 | B.21 | C.34 | D.55 |
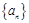 的各项均为正数,且
的各项均为正数,且 ,则
,则








 中,
中, ,
, ,则
,则