题目内容
已知函数 的定义域为
的定义域为 ,值域为[-5,4].
,值域为[-5,4].(Ⅰ)求m、n的值;
(Ⅱ)在△ABC中,
 ,求函数
,求函数 的值域.
的值域.
【答案】分析:(1)利用三角函数的恒等变换求出函数f(x)的解析式为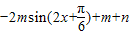 ,分m>0和m<0两种情况,根据函数的定义域求出值域,结合值域求出m、n的值.
,分m>0和m<0两种情况,根据函数的定义域求出值域,结合值域求出m、n的值.
(2)根据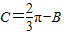 ,得
,得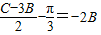 ,分m=3,n=-2和m=-3,n=1两种情况,根据B的范围求出sinB的范围,从而求出函数的值域.
,分m=3,n=-2和m=-3,n=1两种情况,根据B的范围求出sinB的范围,从而求出函数的值域.
解答:解:(1)∵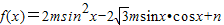 =
=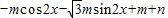
=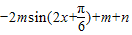 ,
,
由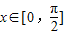 可得,
可得,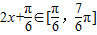 ,
,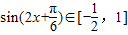 ,
,
若m>0,f(x)∈[-m+n,2m+n],则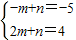 ,∴m=3,n=-2.
,∴m=3,n=-2.
若m<0,f(x)∈[2m+n,-m+n],则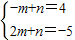 ,m=-3,n=1.
,m=-3,n=1.
(2)∵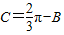 ,∴
,∴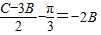 .
.
当m=3,n=-2时,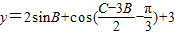 =2sinB+cos2B+3=-2sin2B+2sinB+4=
=2sinB+cos2B+3=-2sin2B+2sinB+4=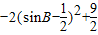 .
.
∵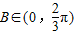 ,∴sinB∈(0,1],
,∴sinB∈(0,1], .
.
当m=-3,n=1时,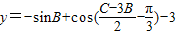 =-sinB+cos2B-3=-2sin2B-sinB-2=
=-sinB+cos2B-3=-2sin2B-sinB-2=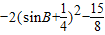 .
.
∵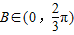 ,
,
∴sinB∈(0,1],y∈[-5,-2).
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,用待定系数法求函数的解析式,体现了分类讨论的数学思想,属于中档题.
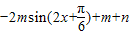 ,分m>0和m<0两种情况,根据函数的定义域求出值域,结合值域求出m、n的值.
,分m>0和m<0两种情况,根据函数的定义域求出值域,结合值域求出m、n的值.(2)根据
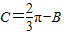 ,得
,得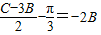 ,分m=3,n=-2和m=-3,n=1两种情况,根据B的范围求出sinB的范围,从而求出函数的值域.
,分m=3,n=-2和m=-3,n=1两种情况,根据B的范围求出sinB的范围,从而求出函数的值域.解答:解:(1)∵
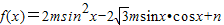 =
=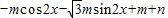
=
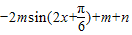 ,
,由
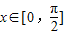 可得,
可得,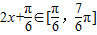 ,
,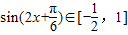 ,
,若m>0,f(x)∈[-m+n,2m+n],则
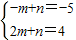 ,∴m=3,n=-2.
,∴m=3,n=-2.若m<0,f(x)∈[2m+n,-m+n],则
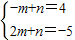 ,m=-3,n=1.
,m=-3,n=1.(2)∵
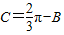 ,∴
,∴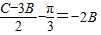 .
.当m=3,n=-2时,
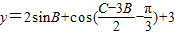 =2sinB+cos2B+3=-2sin2B+2sinB+4=
=2sinB+cos2B+3=-2sin2B+2sinB+4=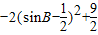 .
.∵
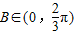 ,∴sinB∈(0,1],
,∴sinB∈(0,1], .
.当m=-3,n=1时,
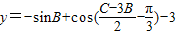 =-sinB+cos2B-3=-2sin2B-sinB-2=
=-sinB+cos2B-3=-2sin2B-sinB-2=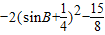 .
.∵
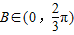 ,
,∴sinB∈(0,1],y∈[-5,-2).
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,用待定系数法求函数的解析式,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为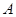 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.