题目内容
若log 2(3-x)+log 0.5(
)<0,则x的取值范围是 .
| 1 | 3x-1 |
分析:log 2(3-x)+log 0.5(
)<0,可化为log2(3-x)(3x-1)<0,进而可化为
,解出即可.
| 1 |
| 3x-1 |
|
解答:解:log 2(3-x)+log 0.5(
)<0,
即log2(3-x)-log2
<0,
∴log2(3-x)(3x-1)<0,
∴
,
解得
<x<3,
故答案为:
<x<3.
| 1 |
| 3x-1 |
即log2(3-x)-log2
| 1 |
| 3x-1 |
∴log2(3-x)(3x-1)<0,
∴
|
解得
5+
| ||
| 3 |
故答案为:
5+
| ||
| 3 |
点评:本题考查对数的运算性质及对数不等式的求解,对数不等式往往转化为不等式组求解,注意真数大于零.

练习册系列答案
相关题目
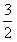 ,2)
,2) 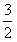 ,+∞)
,+∞) 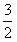 )
)