题目内容
（选修4-3：坐标系与参数方程）已知圆的极坐标方程为：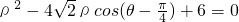
．
（1）将极坐标方程化为普通方程；
（2）若点P（x，y）在该圆上，求x+y的最大值和最小值．
解：（1）由圆的极坐标方程为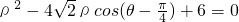：，可得 ρ2-4
ρ（
cosθ+sinθ）+6=0，
化为直角坐标方程为 x2+y2-4x-4y+6=0．
（2）圆的方程即 （x-2）2+（y-2）2=2，表示以（2，2）为圆心，半径等于的圆．
由于点P（x，y）在该圆上，设x=2+cosθ y=2+sinθ，则x+y=4+（sinθ+cosθ）=4+2sin（θ+
），
故x+y的最大值为4+2=6，最小值为4-2=2．
分析：把圆的极坐标方程化为直角坐标方程，再根据圆的标准方程求得圆的参数方程，利用两角和差的正弦公式化简x+y的解析式为4+2sin（θ+），利用正弦函数的值域，求得x+y的最大值和最小值．
点评：本题主要考查把圆的极坐标方程化为直角坐标方程，圆的标准方程和圆的参数方程，两角和差的正弦公式、
正弦函数的值域，属于中档题．
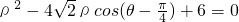，可得 ρ2-4ρ（cosθ+sinθ）+6=0，化为直角坐标方程为 x2+y2-4x-4y+6=0．
（2）圆的方程即 （x-2）2+（y-2）2=2，表示以（2，2）为圆心，半径等于
的圆．由于点P（x，y）在该圆上，设x=2+
cosθ y=2+sinθ，则x+y=4+（sinθ+cosθ）=4+2sin（θ+），故x+y的最大值为4+2=6，最小值为4-2=2．
分析：把圆的极坐标方程化为直角坐标方程，再根据圆的标准方程求得圆的参数方程，利用两角和差的正弦公式化简x+y的解析式为4+2sin（θ+
），利用正弦函数的值域，求得x+y的最大值和最小值．点评：本题主要考查把圆的极坐标方程化为直角坐标方程，圆的标准方程和圆的参数方程，两角和差的正弦公式、
正弦函数的值域，属于中档题．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
选做题在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．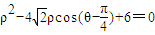
．
∠OAC．
，向量
．求向量
，使得A2
=
．
，焦距为2，求实数a的值．
（a，b．c为实数）的最小值为m，若a-b+2c=3，求m的最小值．