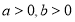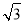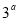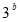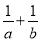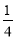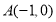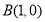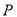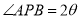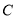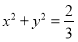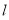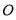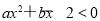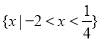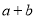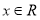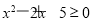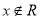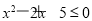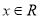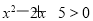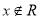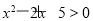题目内容
设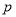 :实数
:实数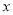 满足
满足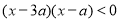 ,其中
,其中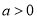 ,
,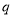 :实数
:实数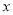 满足
满足 .
.
(1)当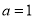 ,
,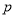 且
且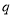 为真时,求实数
为真时,求实数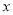 的取值范围;
的取值范围;
(2)若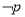 是
是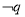 的充分不必要条件,求实数
的充分不必要条件,求实数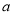 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先求出每个命题为真时的范围,然后根据 列出关于
列出关于 的不等式求解即可;(2)依题意知
的不等式求解即可;(2)依题意知 是
是 的充分不必要条件,由充分不必要条件与集合的关系,得出命题
的充分不必要条件,由充分不必要条件与集合的关系,得出命题 所表示的集合是命题
所表示的集合是命题 所表示集合的真子集,从中求解即可.
所表示集合的真子集,从中求解即可.
试题解析:(1)当 =1时,
=1时, :
: ,
, :
: 4分
4分
∵ 为真 ∴
为真 ∴ 满足
满足 ,即
,即 6分
6分
(2)由 是
是 的充分不必要条件知,
的充分不必要条件知, 是
是 的充分不必要条件 8分
的充分不必要条件 8分
由 知,即A=
知,即A= ,由
,由 知,B=
知,B= 10分
10分
∴B A ∴
A ∴ 且
且 ,即实数
,即实数 的取值范围是
的取值范围是 12分.
12分.
考点:1.二次不等式;2.逻辑联结词;3.充分不必要条件.

练习册系列答案
相关题目