Question

【题目】已知，函数.

（1）当时，解不等式；

（2）若关于的方程的解集中恰有两个元素，求的取值范围；

（3）设，若对任意，函数在区间上的最大值与最小值的和不大于，求的取值范围.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）当a＝1时，利用对数函数的单调性，直接解不等式f（x）1即可；

（2）化简关于x的方程f（x）+2x＝0，通过分离变量推出a的表达式，通过解集中恰有两个元素，利用二次函数的性质，即可求a的取值范围；

（3）在R上单调递减利用复合函数的单调性，求解函数的最值，∴令，化简不等式，转化为求解不等式的最大值，然后求得a的范围．

（1）当时，，

∴，解得，

∴原不等式的解集为.

（2）方程，

即为，

∴，

∴，

令，则，

由题意得方程在上只有两解，

令, ,

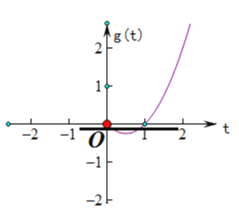
结合图象可得，当时，直线和函数的图象只有两个公共点，

即方程只有两个解．

∴实数的范围.

（3）∵函数在上单调递减，

∴函数在定义域内单调递减，

∴函数在区间上的最大值为，

最小值为，

∴，

由题意得，

∴恒成立，

令，

∴对，恒成立，

∵在上单调递增，

∴

∴，

解得，

又，

∴．

∴实数的取值范围是.