题目内容
(本小题满分l4分)如图, 是抛物线
是抛物线 :
: 上横坐标大于零的一点,直线
上横坐标大于零的一点,直线 过点
过点 并与抛物线
并与抛物线 在点
在点 处的切线垂直,直线
处的切线垂直,直线 与抛物线
与抛物线 相交于另一点
相交于另一点 .
.
(1)当点 的横坐标为2时,求直线
的横坐标为2时,求直线 的方程;
的方程;
(2)若 ,求过点
,求过点 的圆的方程.
的圆的方程.

【答案】
解:(Ⅰ)把 2代入
2代入 ,得
,得 2,
2,
∴点坐 标为(2,2). ……………………1分
标为(2,2). ……………………1分
由  , ①
得
, ①
得
 ,
,
∴过点 的切线的斜率
的切线的斜率
 2,……………………2分
2,……………………2分
直线 的斜率
的斜率



 ……………………3分
……………………3分
∴直线 的方程为
的方程为

 , 即
, 即 ……………………4分
……………………4分
(Ⅱ)设 则
则
∵ 过点 的切线斜率
的切线斜率
 ,因为
,因为
∴ 直线 的斜率
的斜率



 ,
,
直线 的方程为
的方程为 
 ②……………………5分
②……………………5分
设 ,且
,且 为
为 的中点,
的中点,
因为 ,所以过点
,所以过点 的圆的圆心为
的圆的圆心为
半径为 ,……………………6分
,……………………6分
且 ,……………………8分
,……………………8分
所以 (舍去)或
(舍去)或 ……………………9分
……………………9分
联立①②消去 ,得
,得 由题意知
由题意知 为方程的两根,
为方程的两根,
所以 ,又因为
,又因为 ,
所以
,
所以 ,
, ;
;
所以 ,
, ……………………11分
……………………11分
∵ 是
是 的中点,∴
的中点,∴ ……………………12分
……………………12分

 ……………………13分
……………………13分
所以过点 的圆的方程的方程为
的圆的方程的方程为
 ……………………14分
……………………14分
【解析】略

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 ,
, (
( )
) ,证明:
,证明: .
. 的正方体
的正方体 中,
中, 是
是 的中点,
的中点, 在线段
在线段 上,且
上,且 .
. 与
与 所成角的余弦值;
所成角的余弦值; 面
面 ;
; 到面
到面
 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
,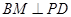 于点
于点 .
.
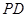 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.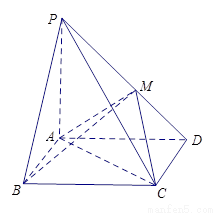
 有唯一的零点
有唯一的零点 .
.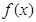 的表达式;
的表达式; 上具有单调性,求实数
上具有单调性,求实数 的取值范围;
的取值范围; (其中
(其中 )的图象如下图所示。
)的图象如下图所示。
 ,
, 及
及 的值;
的值;
 ,且
,且 ,求
,求 的值.。
的值.。