题目内容
以椭圆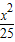 +
+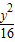 =1的顶点为顶点,离心率为2的双曲线方程( )
=1的顶点为顶点,离心率为2的双曲线方程( )A.
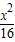 -
-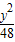 =1
=1B.
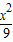 -
-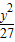 =1
=1C.
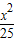 -
-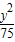 =1或
=1或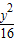 -
-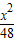 =1
=1D.以上都不对
【答案】分析:确定椭圆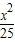 +
+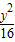 =1的顶点坐标,利用离心率为2,求出几何量,即可得到双曲线的方程.
=1的顶点坐标,利用离心率为2,求出几何量,即可得到双曲线的方程.
解答:解:椭圆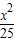 +
+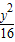 =1的顶点坐标为(±5,0),(0,±4)
=1的顶点坐标为(±5,0),(0,±4)
∵离心率为2,∴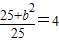 或
或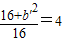
∴b2=75或b′2=48
∴以椭圆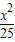 +
+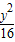 =1的顶点为顶点,离心率为2的双曲线方程为
=1的顶点为顶点,离心率为2的双曲线方程为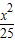 -
-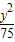 =1或
=1或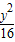 -
-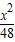 =1
=1
故选C.
点评:本题考查椭圆的标准方程,考查双曲线的方程,考查学生的计算能力,属于基础题.
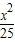 +
+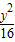 =1的顶点坐标,利用离心率为2,求出几何量,即可得到双曲线的方程.
=1的顶点坐标,利用离心率为2,求出几何量,即可得到双曲线的方程.解答:解:椭圆
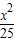 +
+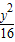 =1的顶点坐标为(±5,0),(0,±4)
=1的顶点坐标为(±5,0),(0,±4)∵离心率为2,∴
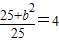 或
或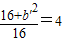
∴b2=75或b′2=48
∴以椭圆
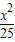 +
+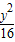 =1的顶点为顶点,离心率为2的双曲线方程为
=1的顶点为顶点,离心率为2的双曲线方程为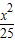 -
-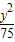 =1或
=1或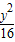 -
-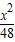 =1
=1故选C.
点评:本题考查椭圆的标准方程,考查双曲线的方程,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 +
+ =1的顶点为顶点,离心率为2的双曲线方程( )
=1的顶点为顶点,离心率为2的双曲线方程( ) -
- =1
=1 -
- =1
=1 -
- =1或
=1或 -
- =1
=1 +
+ =1的顶点为焦点,焦点为顶点的双曲线方程.
=1的顶点为焦点,焦点为顶点的双曲线方程.