题目内容
8.已知函数f(x)=x+$\frac{4}{x}$(1)判断f(x)的奇偶性;
(2)证明f(x)在区间[2,+∞)上是增函数.
分析 (1)先求f(x)定义域为{x|x≠0},容易得到f(-x)=-f(x),从而f(x)为奇函数;
(2)根据增函数的定义,设任意的x1>x2≥2,然后作差,通分,提取公因式x1-x2,从而证明f(x1)>f(x2),这便可得出f(x)在[2,+∞)上是增函数.
解答 解:(1)f(x)的定义域为{x|x≠0};
f(-x)=-x-$\frac{4}{x}$=-f(x);
∴f(x)为奇函数;
(2)证明:设x1>x2≥2,则:
$f({x}_{1})-f({x}_{2})={x}_{1}+\frac{4}{{x}_{1}}-{x}_{2}-\frac{4}{{x}_{2}}$=$({x}_{1}-{x}_{2})(1-\frac{4}{{x}_{1}{x}_{2}})$;
∵x1>x2≥2;
∴x1-x2>0,x1x2>4,$1-\frac{4}{{x}_{1}{x}_{2}}>0$;
∴$({x}_{1}-{x}_{2})(1-\frac{4}{{x}_{1}{x}_{2}})>0$;
∴f(x1)>f(x2);
∴f(x)在[2,+∞)上是增函数.
点评 考查函数奇偶性的定义,以及判断函数奇偶性的方法和过程,增函数的定义,及根据增函数的定义证明一个函数为增函数的方法和过程,作差的方法比较f(x1),f(x2),作差后是分式的一般要通分,一般要提取公因式x1-x2.

练习册系列答案
相关题目
16.设方程2x=|log2(-x)|的两个根分别为x1,x2,则( )
| A. | x1x2<0 | B. | 0<x1x2<1 | C. | x1x2=1 | D. | x1x2>1 |
18.下列叙述正确的是( )
| A. | 方程x2-2x+1=0的根构成的集合为{1,1} | |
| B. | {x∈R|x2+1=0}={x∈R|$\left\{\begin{array}{l}{2x+4>0}\\{x+3<0}\end{array}\right.$} | |
| C. | 集合M={(x,y)|x+y=5且2x-y=0}表示的集合是{2,3} | |
| D. | 集合{1,2,3}与集合{3,2,1}是不同的集合 |
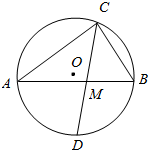 如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.
如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.