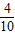题目内容
空间作用在同一点的三个力 两两夹角为60°,大小分别为
两两夹角为60°,大小分别为  ,设它们的合力为
,设它们的合力为 ,则( )
,则( )A.
 ,且与
,且与 夹角余弦为
夹角余弦为 
B.
 ,且与
,且与 夹角余弦为
夹角余弦为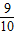
C.
 ,且与
,且与 夹角余弦为
夹角余弦为
D.
 ,且与
,且与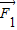 夹角余弦为
夹角余弦为 
【答案】分析:设三个力对应的向量分别为 、
、 、
、 ,以OA、OB、OC为过同一个顶点的三条棱,作平行六面体如图,再以平面OBGC为xoy平面,O为原点、OC为y轴建立如图空间直角坐标系.分别算出点A、B、C的坐标,运用向量的加法法则,可得
,以OA、OB、OC为过同一个顶点的三条棱,作平行六面体如图,再以平面OBGC为xoy平面,O为原点、OC为y轴建立如图空间直角坐标系.分别算出点A、B、C的坐标,运用向量的加法法则,可得 =(-
=(- ,
, ,
, ).最后利用向量模的公式算出|
).最后利用向量模的公式算出| |,并且利用向量夹角公式算出
|,并且利用向量夹角公式算出 与
与 夹角余弦,即得本题答案.
夹角余弦,即得本题答案.
解答:解:设向量 =
= ,
, =
= ,
, =
=

以OA、OB、OC为过同一个顶点的三条棱,
作平行六面体OBGC-ADEF,如图所示
则可得向量 =
=
以平面OBGC为xoy平面,O为原点,
OC为y轴建立空间直角坐标系,如图所示
可得O(0,0,0),B(- ,1,0),C(0,3,0)
,1,0),C(0,3,0)
设A(x,y,z),可得 ,解之得x=-
,解之得x=- ,y=
,y= ,z=
,z= .
.
∴ =
= =(-
=(- ,
, ,
, ),
),
结合 =
= =(-
=(- ,1,0),
,1,0), =
= =C(0,3,0),可得
=C(0,3,0),可得 =(-
=(- ,
, ,
, )
)
∴| |=
|= =5
=5
设 与
与 1所成的角为θ,可得cosθ=
1所成的角为θ,可得cosθ= =
= =
=
即 与
与 1所成角的余弦之值为
1所成角的余弦之值为
故选:C
点评:本题给出空间两两夹角为60°的三个向量,在已知它们的长度情况下求它们的和向量的大小与方向,着重考查了空间向量的坐标运算和向量模与夹角公式等知识,属于中档题.
 、
、 、
、 ,以OA、OB、OC为过同一个顶点的三条棱,作平行六面体如图,再以平面OBGC为xoy平面,O为原点、OC为y轴建立如图空间直角坐标系.分别算出点A、B、C的坐标,运用向量的加法法则,可得
,以OA、OB、OC为过同一个顶点的三条棱,作平行六面体如图,再以平面OBGC为xoy平面,O为原点、OC为y轴建立如图空间直角坐标系.分别算出点A、B、C的坐标,运用向量的加法法则,可得 =(-
=(- ,
, ,
, ).最后利用向量模的公式算出|
).最后利用向量模的公式算出| |,并且利用向量夹角公式算出
|,并且利用向量夹角公式算出 与
与 夹角余弦,即得本题答案.
夹角余弦,即得本题答案.解答:解:设向量
 =
= ,
, =
= ,
, =
=

以OA、OB、OC为过同一个顶点的三条棱,
作平行六面体OBGC-ADEF,如图所示
则可得向量
 =
=
以平面OBGC为xoy平面,O为原点,
OC为y轴建立空间直角坐标系,如图所示
可得O(0,0,0),B(-
 ,1,0),C(0,3,0)
,1,0),C(0,3,0)设A(x,y,z),可得
 ,解之得x=-
,解之得x=- ,y=
,y= ,z=
,z= .
.∴
 =
= =(-
=(- ,
, ,
, ),
),结合
 =
= =(-
=(- ,1,0),
,1,0), =
= =C(0,3,0),可得
=C(0,3,0),可得 =(-
=(- ,
, ,
, )
)∴|
 |=
|= =5
=5设
 与
与 1所成的角为θ,可得cosθ=
1所成的角为θ,可得cosθ= =
= =
=
即
 与
与 1所成角的余弦之值为
1所成角的余弦之值为
故选:C
点评:本题给出空间两两夹角为60°的三个向量,在已知它们的长度情况下求它们的和向量的大小与方向,着重考查了空间向量的坐标运算和向量模与夹角公式等知识,属于中档题.

练习册系列答案
相关题目
 两两夹角为60°,大小分别为
两两夹角为60°,大小分别为  ,设它们的合力为
,设它们的合力为 ,则( )
,则( ) ,且与
,且与 夹角余弦为
夹角余弦为 
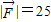 ,且与
,且与 夹角余弦为
夹角余弦为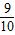
 ,且与
,且与 夹角余弦为
夹角余弦为
 ,且与
,且与 夹角余弦为
夹角余弦为