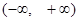题目内容
设 ,若函数
,若函数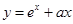 ,
,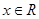 ,有大于零的极值点,则( )
,有大于零的极值点,则( )
A.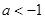 | B.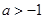 | C.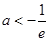 | D.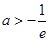 |
A
解析试题分析:先对函数进行求导令导函数等于0,原函数有大于0的极值故导函数等于0有大于0的根,然后转化为两个函数观察交点,确定a的范围.解:∵y=ex+ax,
∴y'=ex+a.由题意知ex+a=0有大于0的实根,令y1=ex,y2=-a,则两曲线交点在第一象限,结合图象易得-a>1⇒a<-1,
故选A.
考点:函数的极值与其导函数
点评:本题主要考查函数的极值与其导函数的关系,即函数取到极值时一定有其导函数等于0,但反之不一定成立.

练习册系列答案
相关题目
已知函数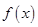 在R上可导,且
在R上可导,且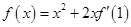 ,则
,则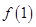 与
与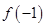 的大小关系是( )
的大小关系是( )
| A.f (-1 ) =" f" ( 1 ) | B.f (-1 ) < f ( 1 ) |
| C.f (-1) > f ( 1 ) | D.不能确定 |
函数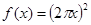 的导数是( )
的导数是( )
A.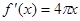 | B.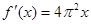 | C.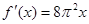 | D.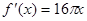 |
函数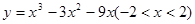 有 ( )
有 ( )
| A.极大值为5,极小值为-27 | B.极大值为5,极小值为-11 |
| C.极大值为5,无极小值 | D.极小值为-27,无极大值 |
已知函数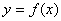 在
在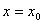 处可导,则
处可导,则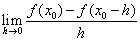 等于
等于
A.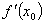 | B.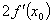 | C.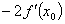 | D.0 |
若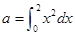 ,
, ,
,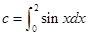 ,则
,则 、
、 、
、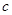 的大小关系是( )
的大小关系是( )
A.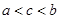 | B.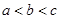 | C.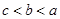 | D.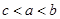 |
已知函数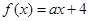 ,若
,若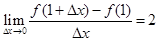 ,则实数
,则实数 的值为( )
的值为( )
A.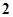 | B.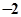 | C.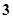 | D.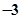 |
已知函数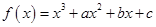 ,若
,若 在区间
在区间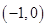 上单调递减,则
上单调递减,则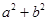 的取值范围是C
的取值范围是C
A.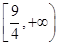 | B.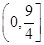 | C.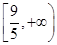 | D.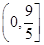 |
 为曲线
为曲线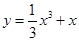 上的任意一点,在点
上的任意一点,在点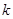 ,则
,则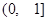 B
B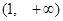 C.
C.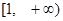 D.
D.