题目内容
函数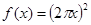 的导数是( )
的导数是( )
A.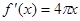 | B.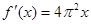 | C.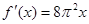 | D.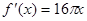 |
C
解析试题分析:因为,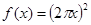 ,所以,其导数为
,所以,其导数为 ,故选C。
,故选C。
考点:导数的计算。
点评:简单题,利用求导公式可得。

练习册系列答案
相关题目
“函数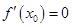 ”是“可导函数
”是“可导函数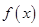 在点
在点 处取到极值”的 条件。 ( )
处取到极值”的 条件。 ( )
| A.充分不必要 | B.必要不充分 | C.充要 | D.既不充分也不必要 |
函数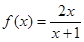 在[1,2]的最大值和最小值分别是 ( )
在[1,2]的最大值和最小值分别是 ( )
A.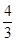 ,1 ,1 | B.1,0 | C.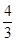 , ,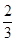 | D.1,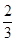 |
若曲线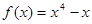 在点P处的切线平行于直线
在点P处的切线平行于直线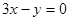 ,则点P的坐标为 ( )
,则点P的坐标为 ( )
| A.(1,0) | B.(1,5) | C.(1,-3) | D.(-1,2) |
已知函数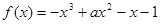 在
在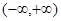 上是单调函数,则实数a的取值范围是( )
上是单调函数,则实数a的取值范围是( )
A.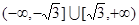 | B.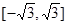 |
C.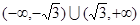 | D.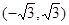 |
设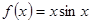 ,
,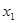 、
、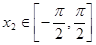 ,且
,且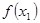 >
>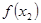 ,则下列结论必成立的是( )
,则下列结论必成立的是( )
A.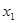 > >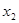 | B.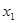 + +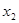 >0 >0 | C.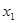 < <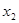 | D.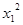 > > |
若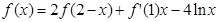 ,则
,则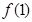 等于( )
等于( )
A.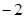 | B.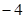 | C.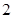 | D.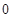 |
设 ,若函数
,若函数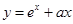 ,
,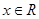 ,有大于零的极值点,则( )
,有大于零的极值点,则( )
A.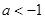 | B.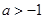 | C.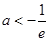 | D.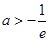 |
函数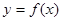 在一点的导数值为
在一点的导数值为 是函数
是函数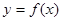 在这点取极值的( )
在这点取极值的( )
| A.充分条件 | B.必要条件 | C.必要非充分条件 | D.充要条件 |