题目内容
求函数y=x2+
思路分析:求函数的单调区间(亦即判断函数的单调性),一般有三种方法:
(1)图象法;(2)定义法;(3)利用已知函数的单调性.
但本题图象不易作,利用y=x2与y=![]() 的单调性也难以确定,故只有用单调性定义来确定,即判断f(x2)-f(x1)的正负.
的单调性也难以确定,故只有用单调性定义来确定,即判断f(x2)-f(x1)的正负.
解:首先确定定义域:{x|x∈R且x≠0},
f(x2)-f(x1)=x22+![]() -x12-
-x12-![]() =(x22-x12)+
=(x22-x12)+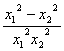 =(x22-x12)(1-
=(x22-x12)(1-![]() ),
),
(1)当x1、x2∈(0,1),x1<x2
时,1-![]() <0,
<0,
∴f(x2)-f(x1)<0,为减函数.
(2)当x1、x2∈(1,+∞),x1<x2时,1-![]() >0,
>0,
∴f(x2)-f(x1)>0,为增函数.同理可求:
(3)当x1、x2∈(-1,0),x1<x2时,为减函数;
(4)当x1、x2∈(-∞,-1),x1<x2时,为增函数.
温馨提示
解答本题易出现以下错误结论:f(x)在(-1,0)∪(0,1)上是减函数,在(-∞,-1)∪(1,+∞)上是增函数,或说f(x)在(-∞,0)∪(0,+∞)上是单调函数,排除障碍是要正确理解函数的单调性概念:函数的单调性是对某个区间而言的,不是两个或两个以上不相交区间的并.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的值域.;
的值域.;