题目内容
【题目】已知正四棱柱ABCD﹣A1B1C1D1中，AB=2，AA1=4． 
（Ⅰ）求证：BD⊥A1C；
（Ⅱ）求二面角A﹣A1C﹣D1的余弦值；
（Ⅲ）在线段CC1上是否存在点P，使得平面A1CD1⊥平面PBD，若存在，求出 
的值；若不存在，请说明理由．
【答案】（Ⅰ）证明：∵ABCD﹣A1B1C1D1为正四棱柱，
∴AA1⊥平面ABCD，且ABCD为正方形．
∵BD平面ABCD，∴BD⊥AA1，BD⊥AC
∵AA1∩AC=A，∴BD⊥平面A1AC．
∵A1C平面A1AC，
∴BD⊥A1C．
（Ⅱ）解：如图，以D为原点建立空间直角坐标系D﹣xyz．
则D（0，0，0），A（2，0，0），C（0，2，0），A1（2，0，4），B1（2，2，4），
C1（0，2，4），D1（0，0，4），
∵ 
=（2，0，0）， 
=（0，2，﹣4）．
设平面A1D1C的法向量 
=（x1，y1，z1）．
∴ 
．即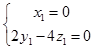 
，
令z1=1，则y1=2．∴ =（0，2，1）．
由（Ⅰ）知平面AA1C的法向量为 
=（2，2，0）
∴cos＜ 
＞= 
= 
．
∵二面角A﹣A1C﹣D1为钝二面角，
∴二面角A﹣A1C﹣D1的余弦值为﹣ ．
（Ⅲ）解：设P（x2，y2，z2）为线段CC1上一点，且 
= 
．
∵ =（x2，y2﹣2，z2）， 
=（﹣x2，2﹣y2，4﹣z2）．
∴（x2，y2﹣2，z2）=λ（﹣x2，2﹣y2，4﹣z2）．
即 
．
∴P（0，2， 
）．
设平面PBD的法向量 
．
∵ 
， 
，
∴ 
．即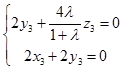 
．
令y3=1，得 
=（﹣1，1，﹣ 
）．
若平面A1CD1⊥平面PBD，则 
=0．
即2﹣ =0，解得 
．
所以当 
= 
时，平面A1CD1⊥平面PBD
【解析】（Ⅰ）由已知条件推导出BD⊥AA1，BD⊥AC，从而得到BD⊥平面A1AC，由此能证明BD⊥A1C．（Ⅱ） 以D为原点建立空间直角坐标系D﹣xyz，利用向量法能求出二面角A﹣A1C﹣D1的余弦值．（Ⅲ）设P（x2，y2，z2）为线段CC1上一点，且 
= 
，利用向量法能求出当 
= 
时，平面A1CD1⊥平面PBD．
【考点精析】根据题目的已知条件，利用直线与平面平行的性质和直线与平面垂直的性质的相关知识可以得到问题的答案，需要掌握一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行；垂直于同一个平面的两条直线平行．
