题目内容
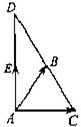如图，△ABC中，AB=4，AC=4，∠BAC=60°，延长CB到D，使|| BA |
| BD |
| AE |
| AB |
| AC |
| A、1 | ||
B、
| ||
| C、3 | ||
D、2
|
分析：先设
=t
，然后用向量
、
表示出向量
，即可找到λ和μ的关系，得到答案．
| AE |
| AD |
| AB |
| AC |
| AE |
解答：解：设
=t
，t∈[0，1]
则
=t
=t(
+
)=t
+t（2
）
=t
+2t（
-
）=2t
-t
∴λ=2t，μ=-t
∴λ-μ=3t
∵t∈[0，1]
∴λ-μ的最大值为3
故选C．
| AE |
| AD |
则
| AE |
| AD |
| AC |
| CD |
| AC |
| CB |
=t
| AC |
| AB |
| AC |
| AB |
| AC |
∴λ=2t，μ=-t
∴λ-μ=3t
∵t∈[0，1]
∴λ-μ的最大值为3
故选C．
点评：本题主要考查平面向量的基本定理，即平面内任一向量都可由任意两不共线的向量唯一表示出来．属中档题．
练习册系列答案
相关题目
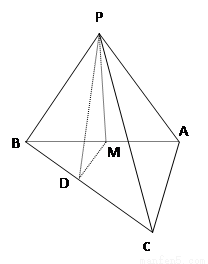
如图，△ABC中，∠A=90°，AB=4，AC=3，平面ABC外一点P在平面ABC内的射影是AB中点M，二面角P-AC-B的大小为45°．
如图在△ABC中，AB⊥AC，
