题目内容
若把函数y=lnx的图象绕原点O逆时针旋转一个α角后与y轴相切,则tanα=( )A.
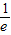
B.e
C.-e
D.-
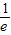
【答案】分析:设y=lnx的图象的切线的斜率为k,切点坐标为(x,y),由题意可得 k= =
= ,求得x=e.由此能求出tanθ.
,求得x=e.由此能求出tanθ.
解答:解:利用函数的图象绕坐标原点O逆时针旋转一个α角后与y轴相切,
知函数y=lnx的一条切的倾斜角为 ,
,
设y=f(x)=lnx的图象的切线的斜率为k,设切点坐标为(x,y),
则由题意可得,切线的斜率为 k= =
= ,
,
∵y=lnx,
∴ ,
,
再由导数的几何意义可得 k=f′(x)= ,
,
∴ =
= ,∴x=e.
,∴x=e.
再由α的意义可得,tanα=cot( )=
)= =x=e.
=x=e.
故选B.
点评:本题主要考查函数的导数的意义及其应用,直线的斜率公式,函数图象的变化,属于基础题.
 =
= ,求得x=e.由此能求出tanθ.
,求得x=e.由此能求出tanθ.解答:解:利用函数的图象绕坐标原点O逆时针旋转一个α角后与y轴相切,
知函数y=lnx的一条切的倾斜角为
 ,
,设y=f(x)=lnx的图象的切线的斜率为k,设切点坐标为(x,y),
则由题意可得,切线的斜率为 k=
 =
= ,
,∵y=lnx,
∴
 ,
,再由导数的几何意义可得 k=f′(x)=
 ,
,∴
 =
= ,∴x=e.
,∴x=e.再由α的意义可得,tanα=cot(
 )=
)= =x=e.
=x=e.故选B.
点评:本题主要考查函数的导数的意义及其应用,直线的斜率公式,函数图象的变化,属于基础题.

练习册系列答案
相关题目