题目内容
设平面内有
、
、
、
四个向量,满足
=
-
,
=2
-
,
⊥
,|
|=|
|=1,设θ为
,
的夹角,则cosθ=
.
| a |
| b |
| x |
| y |
| a |
| y |
| x |
| b |
| x |
| y |
| a |
| b |
| a |
| b |
| x |
| y |
3
| ||
| 10 |
3
| ||
| 10 |
分析:由向量
、
的表示
、
,结合已知条件可计算出
和
的大小,据此结合
•
=0,即(
-
)(2
-
)=0,可得
•
的值,最后利用向量数量积的定义,即可得出cosθ的值.
| a |
| b |
| x |
| y |
| |x| |
| |y| |
| a |
| b |
| y |
| x |
| x |
| y |
| x |
| y |
解答:解:由
,得
∵
⊥
,
=
=1
∴
2=
2=1,
•
=0,
可得
=
=
,
=
=
∵
•
=(
-
)(2
-
)=0,即-2×2+3
•
-5=0,得
•
=3
∴
、
的夹角θ满足:cosθ=
=
故答案为:
|
|
∵
| a |
| b |
| |a| |
| |b| |
∴
| a |
| b |
| a |
| b |
可得
| |x| |
(
|
| 2 |
| |y| |
(2
|
| 5 |
∵
| a |
| b |
| y |
| x |
| x |
| y |
| x |
| y |
| x |
| y |
∴
| x |
| y |
| ||||
|
3
| ||
| 10 |
故答案为:
3
| ||
| 10 |
点评:本题给出两个向量方程组,在已知一组单位向量互相垂直的情况下求另一组向量的夹角余弦值.着重考查了向量加减混合运算及其几何意义和向量数量积公式、模的公式和夹角公式,属于基础题.

练习册系列答案
相关题目
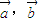 满足:
满足: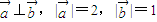 ,点M(x,y)的坐标满足:
,点M(x,y)的坐标满足: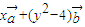 与
与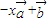 互相垂直.求证:平面内存在两个定点A、B,使对满足条件的任意一点M均有|
互相垂直.求证:平面内存在两个定点A、B,使对满足条件的任意一点M均有| 等于定值.
等于定值.