题目内容
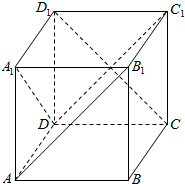
1．在正方体ABCD-A1B1C1D1中，过DD1的中点作直线l，使得l与BD1所成角为40°，且与平面A1ACC1所成角为50°，则l的条数为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 无数 |
分析 取DD1的中点P，A1C1的中点为O1，AC的中点为O2，O1O2的中点为O，连结OP和PO2，则OP⊥平面ACC1A1，PO2∥BD1．在平面ACC1A1内，以点O为圆心，半径为$\frac{\frac{\sqrt{2}}{2}}{tan50°}$画圆，即可得出结论．
解答 
解：取DD1的中点P，A1C1的中点为O1，AC的中点为O2，O1O2的中点为O，连结OP和PO2，则OP⊥平面ACC1A1，PO2∥BD1．
在平面ACC1A1内，以点O为圆心，半径为$\frac{\frac{\sqrt{2}}{2}}{tan50°}$画圆，则点P与此圆上的点的连线满足：过DD1的中点P与平面ACC1A1所成的角为50°．所以满足与PO2所成角为40°的直线PQ有且只有2条，
故选：B．
点评 本题考查线面角，考查学生分析解决问题的能力，有难度．
练习册系列答案
相关题目
11．点M（5，3）到抛物线y=ax2的准线的距离为6，那么抛物线的标准方程是（ ）
| A． | x2=$\frac{1}{12}$y | B． | x2=$\frac{1}{12}$y或x2=-$\frac{1}{36}$y | ||
| C． | x2=-$\frac{1}{36}$y | D． | x2=12或x2=-36y |
已知如图所示的非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，请分别作出满足下列条件的向量$\overrightarrow{c}$．
四面体ABCD中，AD⊥平面ABC，AB⊥BC，E，F分别为AC，BD的中点，AB=AD=2，∠BAC=60°．
13．下列四个函数中，在（-∞，0）上是增函数的为（ ）
| A． | f（x）=x2+4 | B． | f（x）=3-$\frac{2}{x}$ | C． | f（x）=x2-5x-6 | D． | f（x）=1-x |