题目内容

在正三角形ABC中，AB=2，设点P、Q满足：
AP
=λ
AB
，
AQ
=（1-λ）
AC
（λ为实数），若
BQ
•
CP
=-
3
2
，则λ等于（　　）
分析：
BQ
•
CP
=（
AQ
-
AB
）•（
AP
-
AC
），代入
AP
=λ
AB
，
AQ
=（1-λ）
AC
可化为
AB
、
AC
的数量积运算，化简可得λ的方程，解出即得答案．
解答：解：在正三角形ABC中，AB=2，则
AB
•
AC
=|
AB
|×|
AC
|cos60°=2×2×
1
2
=2，
∴
BQ
•
CP
=（
AQ
-
AB
）•（
AP
-
AC
）=
AQ
•
AP
-
AQ
•
AC
-
AB
•
AP
+
AB
•
AC

=（1-λ）
AC
•λ
AB
-（1-λ）
AC
•
AC
-
AB
•λ
AB
+
AB
•
AC

=（1-λ）λ×2×2cos60°-（1-λ）×2×2-2×2λ+2×2cos60°
=-2λ2+2λ-2=-
3
2
，解得λ=
1
2
，
故选A．
点评：本题考查平面向量的数量积运算，考查学生的运算能力，属基础题．
练习册系列答案
相关题目
197、已知结论“在正三角形ABC中，若D是边BC中点，G是三角形ABC的重心，则AG：GD=2：1”，如果把该结论推广到空间，则有命题
“在正四面体ABCD中，若M是底面BCD的中心，O是正四面体ABCD的中心，则AO：OM=3：1．”
．
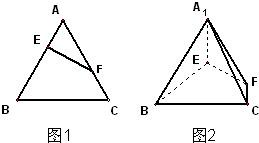精英家教网在正三角形ABC中，E、F分别是AB、AC边上的点，满足
AE
EB
=
CF
FA
=
1
2
（如图1）．将△AEF沿EF折起到△A1EF的位置，使二面角A1-EF-B成直二面角，连接A1B、A1C． （如图2）求证：A1E⊥平面BEC．
如图，在正三角形ABC中，D，E，F分别为各边的中点，G，J分别为AF，DE的中点．将△ABC沿DE，EF，DF折成三棱锥以后，GJ与DE所成角的度数为（　　）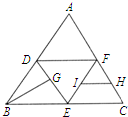
如图，在正三角形ABC中，D，E，F分别为AB，BC，AC的中点，G，H，I分别为DE，FC，EF的中点，将
△ABC沿DE，EF，DF折成三棱锥，则异面直线BG与IH所成的角为（　　）
在正三角形ABC中，D是BC上的点，AB=3，BD=2，则
AB
•
AD
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网