题目内容
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上，其中n=1,2,3,….（Ⅰ）证明数列{lg(1+an)}是等比数列；
（Ⅱ）设Tn=(1+a1)(1+a2)…(1+an),求Tn及数列{an}的通项；
（Ⅲ）记bn=
+
,求数列{bn}的前几项和Sn，并证明Sn+
=1.
解：(Ⅰ)由已知an+1=+2an,
∴an+1+1=(an+1)2.∵a1=2,∴an+1=＞1,两边取对数得：lg(1+an+1)=2lg(an+1),即：=2.
∴{lg(1+an}是公比为2的等比数列.
(Ⅱ)由（Ⅰ)知，lg(1+an)=2n-1·lg(1+a1)=2n-1·lg3=,
∴1+an=
.(*)
∴Tn=(1+a1)(1+a2)…(1+an)=
·
·
·…·
=
=
.由(*)式得 an=
-1.
(Ⅲ)∵an+1=
+2an=an(an+2),
∴
=
(
-
),
∴
=
-
,又bn=
+
,
∴bn=
+
-
=2(
-
）.
∴Sn=b1+b2+…+bn
=2(
-
+
-
+…+
-
)
=2(
-
).
∵an=
-1,a1=2,an+1=
-1,
∴Sn=1-
,又Tn=
,
∴Sn+
=1.
练习册系列答案
相关题目
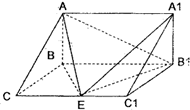如图，直三棱柱ABC-A1B1C1中，AB⊥BC，E为棱CC1的中点，已知AB=