��Ŀ����
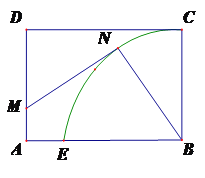
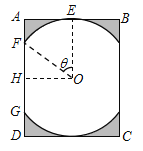
����Ŀ��ij������һ�����Ž������䴰�������ͼ��ʾ.Բ![]() ��Բ�������
��Բ�������![]() �Խ��ߵĽ����غϣ���Բ����������������У�
�Խ��ߵĽ����غϣ���Բ����������������У�![]() Ϊ���е㣩�������������ཻ��
Ϊ���е㣩�������������ཻ��![]() ��
��![]() Ϊ�����������㣩��ͼ����Ӱ����Ϊ�����������ಿ��Ϊ������.��֪Բ�İ뾶Ϊ1
Ϊ�����������㣩��ͼ����Ӱ����Ϊ�����������ಿ��Ϊ������.��֪Բ�İ뾶Ϊ1![]() ����
����![]() ����
����![]() ������������Ϊ
������������Ϊ![]() .
.
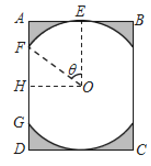
��1����![]() ����
����![]() �ĺ�����ϵʽ�������������
�ĺ�����ϵʽ�������������
��2���������Ҫ������������δ���������ֵԽ��Խ��.���ñ�ֵ���ʱ�����![]() �ij���.
�ij���.
���𰸡���1��![]() ����
����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��������Ϊ
��������Ϊ![]() ��
��
��2������������δ���������ֵ���ʱ��![]() �ij���Ϊ1
�ij���Ϊ1![]() ��
��
�����������������
(1) ����![]() ��
��![]() �ڵ�
�ڵ�![]() ���ɵ�
���ɵ�![]() ����
����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��������Ϊ
��������Ϊ![]() ��
��
(2)��ԭ�����뵼�����Ĺ�ϵ�ɵ���![]() ʱ��
ʱ��![]() �����ֵ
�����ֵ![]() ����ʱ
����ʱ![]()
���������
��:(1) ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��
����![]() ��
��
![]() ��
��
����![]()
![]()
![]() ��
��
��Ϊ![]() ������
������![]() �����Զ�����Ϊ
�����Զ�����Ϊ![]() ��
��
��2�����δ�������Ϊ![]() ��
��
������������δ���������ֵΪ![]() ��
��
��![]() ��
��![]() ��
��
��![]()
![]()
![]()
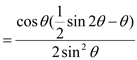 ��
��
��Ϊ![]() ������
������![]() ������
������![]() ����
����![]() ��
��
���Ժ���![]() ��
��![]() �ϵ�������
�ϵ�������
���Ե�![]() ʱ��
ʱ��![]() �����ֵ
�����ֵ![]() ����ʱ
����ʱ![]()
�𣺣�1��![]() ����
����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��������Ϊ
��������Ϊ![]() ��
��
��2������������δ���������ֵ���ʱ��![]() �ij���Ϊ1
�ij���Ϊ1![]() ��
��

����Ŀ����һ�����룬�������������ַ���ɣ������������Ķ�Ӧ�����������ɣ�����������±��������ɱ���ÿһ��ȡһ���ַ���ɣ��ҵ�һ��ȡ���ַ����ڵ�һλ���ڶ���ȡ���ַ����ڵڶ�λ��������ȡ���ַ����ڵ���λ����Ӧ�����������Ķ�Ӧ�����ְ���ͬ�Ĵ����ų�һ�����.
| �����ַ� | A | B | C | D |
�����ַ� | 11 | 12 | 13 | 14 | |
| �����ַ� | E | F | G | H |
�����ַ� | 21 | 22 | 23 | 24 | |
| �����ַ� | M | N | P | Q |
�����ַ� | 1 | 2 | 3 | 4 |
���������![]() ��ʾ�����в�ͬ���ֵĸ�����
��ʾ�����в�ͬ���ֵĸ�����
(��)��![]() �ķֲ��к�������ѧ������
�ķֲ��к�������ѧ������